题目内容
13. 在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.(1)求$\frac{AP}{PB}$的值;
(2)若BD=5,求CQ的长.
分析 (1)设BD=x,根据题意用x表示出CD、AD、BC,根据相似三角形的性质列出比例式,计算即可;
(2)根据勾股定理求出CE,根据三角形中位线定理求出CQ即可.
解答 解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴$\frac{AQ}{CD}$=$\frac{AE}{DE}$=1,
∴AQ=CD=2x,
∴$\frac{AP}{PB}$=$\frac{AQ}{BC}$=$\frac{2}{3}$;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=$\frac{1}{2}$AD=7.5,
由勾股定理得,CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\frac{25}{2}$,
∴CQ=25.
点评 本题平行线分线段成比例的性质、三角形中位线定理,掌握平行线分线段成比例的性质是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
18.阳光实验学校组织学生到新兴陶瓷厂参观陶瓷工艺制作,爱动脑筋的小强同学看到桌子上整齐地摆放着若干相同规格的碟子,通过测量发现碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
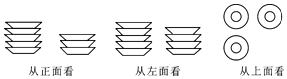
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.
| 碟子的个数 | 碟子的高度(单位:cm) |
| 1 | 2 |
| 2 | 2+1.5 |
| 3 | 2+3 |
| 4 | 2+4.5 |
| … | … |
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.

3.方城七峰山悬空玻璃桥于2016年9月初正式对外开放,吸引无数游客前去观光游玩.在今年的十一黄金周期间,聪聪同学一家四人,慧慧同学一家六人,相约前往七峰山游玩,到景区门口发现一张海报.(聪聪和慧慧两家一共有2名儿童).
成人:a元/张
网上定价:优惠5元
儿童:按成人票价5折优惠
网上定价:优惠3元
团体票:(14人以上含14人)按成人票6折优惠
网上定价:优惠4元
(1)根据以上信息,帮聪聪、慧慧完成以下表格.(用含a的式子表示)
(2)如果a=40元,通过网上定票,哪种方式更合算?
成人:a元/张
网上定价:优惠5元
儿童:按成人票价5折优惠
网上定价:优惠3元
团体票:(14人以上含14人)按成人票6折优惠
网上定价:优惠4元
(1)根据以上信息,帮聪聪、慧慧完成以下表格.(用含a的式子表示)
| 购票方式 票价 | 在景区门票 | 网上定票 |
| 成人的票价(元) | a | a-5 |
| 儿童的票价(元) | $\frac{1}{2}$a | a-3 |
| 团体购票价(元) | a | a-4 |
 如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.