题目内容
9.在△ABC中,∠A=50°,若O为△ABC的外心,∠BOC=100°;若I为△ABC的内心,∠BIC=115°.分析 直接利用三角形内心即角平分线的交点,外心是外接圆圆心,进而得出答案.
解答 解:∵△ABC的内心为I,∠A=50°,
∴∠ABC+∠ACB=130°,
∴∠BIC=180°-$\frac{1}{2}$×130°=115°,
∵O为△ABC的外心,
∴∠BOC═2∠A=100°.
故答案为:100°,115°.
点评 本题考查了圆周角定理,三角形的内切圆和外接圆的应用,注意:同弧或等弧所对圆周角等于它所对圆心角的一半,正确把握内心、外心的定义是解题关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
19.在△ABC和△A'B'C'中,AB=A'B',∠B=∠B',补充条件后仍不一定能保证△ABC≌△A'B'C',则补充的这个条件是( )
| A. | BC=B'C' | B. | ∠A=∠A' | C. | AC=A'C' | D. | ∠C=∠C' |
18.阳光实验学校组织学生到新兴陶瓷厂参观陶瓷工艺制作,爱动脑筋的小强同学看到桌子上整齐地摆放着若干相同规格的碟子,通过测量发现碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.
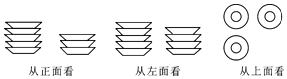
| 碟子的个数 | 碟子的高度(单位:cm) |
| 1 | 2 |
| 2 | 2+1.5 |
| 3 | 2+3 |
| 4 | 2+4.5 |
| … | … |
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.

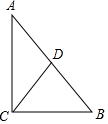 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.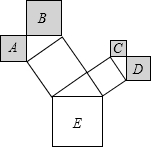 如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38. 如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC. 已知矩形ABCD中,AB=1,在BC上取一点E,将△ABE沿AE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似.由对应边成比例,则可得只含AD的一个比例式$\frac{AD-1}{1}=\frac{1}{AD}$.
已知矩形ABCD中,AB=1,在BC上取一点E,将△ABE沿AE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似.由对应边成比例,则可得只含AD的一个比例式$\frac{AD-1}{1}=\frac{1}{AD}$.