题目内容
12.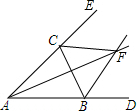 如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )
如图,△ABC外角∠CBD,∠BCE的平分线BF、CF相交于点F,则下列结论成立的是( )| A. | AF平分BC | B. | AF⊥BC | C. | AF平分∠BAC | D. | AF平分∠BFC |
分析 作FP⊥AE于P,FG⊥BC于G,FH⊥AD于H,根据角平分线的性质得到FP=FH,根据角平分线的判定定理判断即可.
解答 解: 作FP⊥AE于P,FG⊥BC于G,FH⊥AD于H,
作FP⊥AE于P,FG⊥BC于G,FH⊥AD于H,
∵CF是∠BCE的平分线,
∴FP=FG,
∵BF是∠CBD的平分线,
∴FH=FG,
∴FP=FH,又FP⊥AE,FH⊥AD,
∴AF平分∠BAC,
故选:C.
点评 本题考查的是角平分线的性质和判定,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
7.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
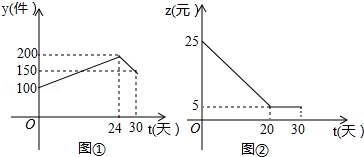

| A. | 第24天的销售量最多 | |
| B. | 20≤t≤30日销售利润不变 | |
| C. | 第30天的日销售利润是750元 | |
| D. | 当0≤t≤24时,设产品日销售量y与时间t的函数关系为y=$\frac{25}{6}$t+100 |
17.估计与$\sqrt{11}$最接近的整数是( )
| A. | 3 | B. | 4 | C. | -3 | D. | ±3 |
4.代数式2016-a2+2ab-b2的最大值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 不存在 |
 如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.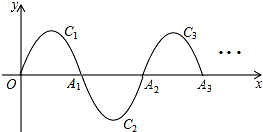 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.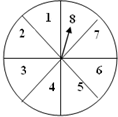 自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.
自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.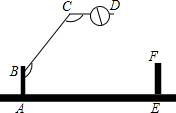 一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.
一个小区大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,那么∠ABC+∠BCD=270度.