题目内容
5. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.(1)求证:FC=AD;
(2)求证:AB=BC+AD;
(3)若∠ABC=50°,求∠F.
分析 (1)可通过说明△ADE≌△FCE,证明FC=AD;
(2)由(1)知,AD=CF,要证明AB=BC+AD,只要证明AB=BF就行.可利用三线合一或者说明△ABE≌△FBE;
(3)由(2)知△ABF是等腰三角形,知∠ABC,利用等腰三角形的角间关系,易求∠F.
解答 解:(1)证明:∵AD∥BC,
∴∠DAE=∠F,∠ADE=∠FCE.
∵点E是DC的中点,
∴DE=CE.
在△ADE和△FCE中$\left\{\begin{array}{l}{∠DAF=∠F}\\{∠ADE=∠FCE}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△FCE,
∴FC=AD.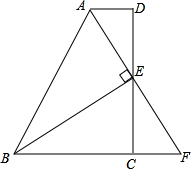
(2)证明:由于△ADE≌△FCE,
∴AE=EF,FC=AD,
又∵BE⊥AF,
∴BE是△ABF的中垂线,
∴AB=BF=BC+CF=BC+AD.
(3)解:由(2)知,△ABF是等腰三角形,
∴∠F=$\frac{180°-∠ABC}{2}=\frac{180°-50°}{2}=65°$.
点评 本题是一道四边形综合题,主要考察了三角形全等的判断,等腰三角形的三线合一和三角形的内角间关系.在等腰三角形中,若已知顶角,则底角=$\frac{180°-顶角}{2}$,若已知底角,顶角=180°-2底角.解决此类问题,前面的结论可作为后面的条件.

练习册系列答案
相关题目
7. 二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论不正确的是( )| A. | a<0 | B. | c>0 | C. | a+b+c>0 | D. | b2-4ac>0 |
20.若样本x1,x2,x3,x4,x5的而平均数为a,则样本3x1-6,3x2-6,3x3-6,3x4-6,3x5-6的平均数为( )
| A. | a | B. | 3a | C. | 3a-6 | D. | 3a+6 |

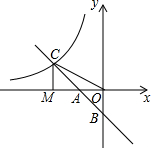 如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )