题目内容
16.定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,若AM=4,求△BMG的面积.

分析 (1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D;
于是得到结果;
(3)由H是DN的中点,等到DH=HN=$\frac{1}{2}$c,通过全等三角形的性质得到DG=EN=b,MG=c-b,由相似三角形的性质得到$\frac{c-b}{b}$=$\frac{a}{a+c}$,求得AM=BN=4,MN=4$\sqrt{2}$,过G作GP⊥AB于P,过E作EQ⊥AB于Q,根据相似三角形的性质得到GP=2$\sqrt{6}$-2$\sqrt{3}$,然后由三角形的面积公式即可得到结论.
解答 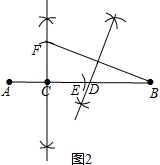 (1)解:①当MN为最大线段时,
(1)解:①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}-A{M}^{2}}$=$\sqrt{9-4}$=$\sqrt{5}$;
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}+A{M}^{2}}$=$\sqrt{9+4}$=$\sqrt{13}$,
综上所述:BN=$\sqrt{5}$或$\sqrt{13}$;
(2)解:作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示:
(3)∵H是DN的中点,
∴DH=HN=$\frac{1}{2}$c,
∵△MND和△NBE均是等边三角形,
∴∠D=∠DNE=60°,
在△DGH和△NEH中,
$\left\{\begin{array}{l}{∠D=∠DNE}\\{DH=HN}\\{∠DHG=∠NHE}\end{array}\right.$,
∴△DGH≌△NEH,
∴DG=EN=b,MG=c-b,
∵GM∥EN,
∴△AGM∽△NEN,
设AM=a,BN=b,MN=c,
∴$\frac{c-b}{b}$=$\frac{a}{a+c}$,
∴c2=2ab-ac+bc,
∵点M,N是线段AB的勾股分割点,
∴c2=a2+b2,
∴(a-b)2=(b-a)c,
∵b-a≠c,
∴a=b,
∴AM=BN=4,
∴MN=4$\sqrt{2}$,
过G作GP⊥AB于P,过E作EQ⊥AB于Q,
∵∠DMN=∠ENB=60°,
∴GM∥EN,
∴△AGM∽△AEN,
∴$\frac{AM}{AN}=\frac{GP}{EQ}$,
∵AM=4,AN=4+4$\sqrt{2}$,EQ=2$\sqrt{3}$,
∴GP=2$\sqrt{6}$-2$\sqrt{3}$,
∴S△BMG=$\frac{1}{2}$BM•GP=$\frac{1}{2}$×(4+4$\sqrt{2}$)×(2$\sqrt{6}$-2$\sqrt{3}$)=4$\sqrt{3}$.
点评 本题是三角形综合题目,考查了新定义“勾股分割点”、勾股定理、三角形中位线定理、全等三角形的判定与性质、相似三角形的判定与性质、等边三角形的性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(3)中,需要证明三角形全等和三角形相似才能得出结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
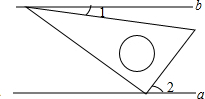 如图,将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a,b上,如果∠2=50°,那么∠1的度数为( )
如图,将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a,b上,如果∠2=50°,那么∠1的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
| A. | 等边三角形 | B. | 等腰直角三角形 | C. | 钝角三角形 | D. | 无法判断形状 |
| A. | 零和正分数 | B. | 零和负分数 | C. | 只有负分数 | D. | 零和分数 |
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.