题目内容
1.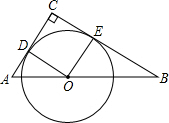 如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.(1)连接OD,OE,求证:△ADO∽△OEB;
(2)当AC=2时,求⊙O的半径;
(3)设AC=x,⊙O的半径为y,求y与x的函数关系式.
分析 (1)由已知条件易证∠A=∠EOB,∠ADO=∠OEB=90°,所以可证明△ADO∽△OEB;
(2)由△ABC是直角三角形,以O为圆心的⊙O分别与AC,BC相切于点D,E,可知OD∥BC,在△ADO中,解得半径即可.
(3)由题意可知,OD∥BC,∠AOD=∠B,则两角正切值相等,进而列出关系式.
解答 (1)证明:∵O为圆心的⊙O分别与AC,BC相切于点D,E,
∴OD⊥AC,OE⊥BC,
∴∠ADO=∠OEB=90°,
∵∠C=90°,
∴OE∥AC,
∴∠A=∠EOB,
∴△ADO∽△OEB;
(2)解:在△ABC中,∠C=90°,AC+BC=8,
∵AC=2,
∴BC=6;
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,
∴四边形OECD是正方形,
tan∠B=tan∠AOD=$\frac{AD}{OD}=\frac{2-OD}{OD}$=$\frac{1}{3}$,
解得OD=1.5,
∴圆的半径为1.5;
(3)解:∵AC=x,BC=8-x,
在直角三角形ABC中,tanB=$\frac{AC}{BC}=\frac{x}{8-x}$
∵以O为圆心的⊙O分别与AC,BC相切于点D,E,
∴四边形OECD是正方形.
tan∠AOD=tanB=$\frac{AC}{BC}=\frac{AD}{OD}$=$\frac{x-y}{y}$,
解得y=-$\frac{1}{8}$x2+x.
点评 本题考查了切线的性质.相似三角形的性质与判定以及锐角三角函数的运用,在运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形,证明三角形相似解决有关问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.用代入法解方程组$\left\{\begin{array}{l}{3x=2y+1}&\\{2x=3y}&\end{array}\right.$,以下各式中,代入正确的是( )
| A. | 3x=2×$\frac{2x}{3}$+1 | B. | 3x=2×$\frac{2y}{3}$+1 | C. | 3x=2×$\frac{3x}{2}$+1 | D. | 3x=2×6x+1 |
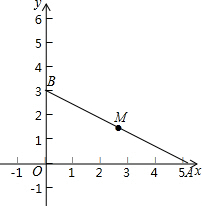 已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.
已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点. 如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.
如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.