题目内容
12.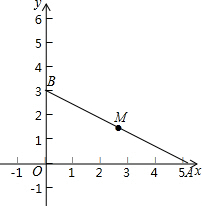 已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.
已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.(1)将△BOM沿OM翻折后点B落在B′,求直线BB′的解析式;
(2)若以点O、B、M、N为顶点的四边形是平行四边形,求点N的坐标.
分析 (1)由点M是AB的中点可求得点M的坐标,依据特殊锐角三角函数值可求得∠BAO=30°,然后依据含30°直角三角形的性质可证得OB=BM,由轴对称图形的性质可知:BM=B′M,OB=OB′,从而可证明四边形BOB′M是菱形.从而可求得B′($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).最后依据待定系数法可求得直线BB′的解析式;
(2)如图2所示:分为MN为四边形的边或MN为四边形的对角线两种情况画出图形,然后依据对边平行且相的等的四边形、对角线互相平分的四边形是平行四边形可确定出点N的坐标.
解答 解:(1)如图1所示: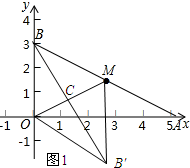
∵A(3$\sqrt{3}$,0),B(0,3),
∴OB=3,OA=3$\sqrt{3}$.
∴tan∠BAO=$\frac{3}{3\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
∴∠BAO=30°.
∴OB=$\frac{1}{2}$AB.
∵M是AB的中点,
∴MB=MA=$\frac{1}{2}$AB.
∴OB=BM.
∵点B与点B′关于OM对称,
∴BM=B′M,OB=OB′.
∴OB=OB′=MB′=MB.
∴四边形BOB′M是菱形.
∴MB′∥OB,MB′=OB=3.
∵M是AB的中点,
∴M($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
∴B′($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
设直线BB′的解析式为y=kx+3.
∵将B′的坐标代入得:$\frac{3\sqrt{3}}{2}k$+3=$-\frac{3}{2}$,解得:k=-$\sqrt{3}$,
∴直线BB′的解析式为y=-$\sqrt{3}$x+3.
(2)如图2所示: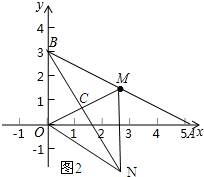
由(1)可知点N的坐标为($\frac{3\sqrt{3}}{2}$,-$\frac{3}{2}$).
如图3所示: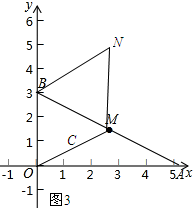
当MN∥OB,且MN=OB时,四边形BOMN为平行四边形,
∵M($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$),OB=MN=3,
∴N($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$).
如图4所示:当CM=CN,BC=OC时,四边形BOMN为平行四边形.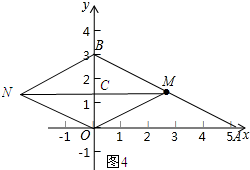
∵M是AB的中点,∠BOA=90°,
∴OM=BM.
又∵BC=OC,
∴MN⊥OB.
又∵NC=CM,
∴点N与点M关于y轴对称.
∴点N的坐标为(-$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、含30度直角三角形的性质、特殊锐角三角函数值、菱形的性质和判定、平行四边形的判定,根据题意画出符合题意得图形是解题的关键.

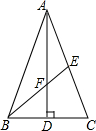 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24. 如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.
如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.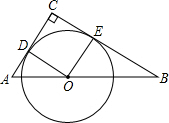 如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.