题目内容
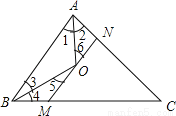
如图,已知△ABC中,AC+BC=24,AO,BO分别是角平分线,且MN∥BA,分别交AC于N,BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
 B
【解析】
试题分析:由AO,BO分别是角平分线求得∠1=∠2,∠3=∠4,利用平行线性质求得,∠1=∠6,∠3=∠5,利用等量代换求得∠2=∠6,∠4=∠5,即可解题.
【解析】
由AO,BO分别是角平分线得∠1=∠2,∠3=∠4,
又∵MN∥BA,∴∠1=∠6,∠3=∠5,
∴∠2=∠6,∠4=∠5,
∴AN=NO,BM=OM.
∵AC+BC=24...
B
【解析】
试题分析:由AO,BO分别是角平分线求得∠1=∠2,∠3=∠4,利用平行线性质求得,∠1=∠6,∠3=∠5,利用等量代换求得∠2=∠6,∠4=∠5,即可解题.
【解析】
由AO,BO分别是角平分线得∠1=∠2,∠3=∠4,
又∵MN∥BA,∴∠1=∠6,∠3=∠5,
∴∠2=∠6,∠4=∠5,
∴AN=NO,BM=OM.
∵AC+BC=24...
练习册系列答案
相关题目
一个不透明的袋中共有20个球,它们除颜色不同外,其余均相同,其中8个白球,5个黄球,5个绿球,2个红球,则任意摸出一个球是红球的概率是( )
A.  B.
B. 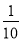 C.
C. 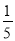 D.
D. 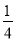
 B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B.
B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B. 在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
 126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角...
126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
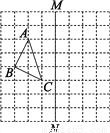
当∠B为钝角... 如图,在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)在网格上的最小正方形的边长为1,求△ABC的面积.
 (1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
(2)S△ABC=2×3-2×(×1×2)-×1×3=.
(1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
(2)S△ABC=2×3-2×(×1×2)-×1×3=. 在“线段、锐角、三角形、等边三角形”这四个图形中,其中是轴对称图形的有___个,其中对称轴最多的是__________.
 3 等边三角形
【解析】线段有两条对称轴,锐角有一条对称轴,等边三角形有三条对称轴,
故答案为:3,等边三角形.
3 等边三角形
【解析】线段有两条对称轴,锐角有一条对称轴,等边三角形有三条对称轴,
故答案为:3,等边三角形. 如图所示的四个图形中,从几何图形变换的角度考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
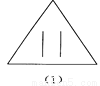
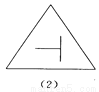
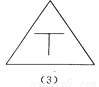
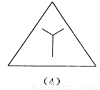
 图(2),仅它不是轴对称图形
【解析】试题分析:观察图形发现(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形,由此即可得出结论.
试题解析:【解析】
(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形.故从几何图形变换的角度考虑,图(2)与其它三个不同.
图(2),仅它不是轴对称图形
【解析】试题分析:观察图形发现(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形,由此即可得出结论.
试题解析:【解析】
(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形.故从几何图形变换的角度考虑,图(2)与其它三个不同. 如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.
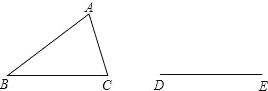
A.2 B.4 C.6 D.8
 B.
【解析】
试题分析:可以做4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.如图.
故选:B.
B.
【解析】
试题分析:可以做4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.如图.
故选:B. 关于x的方程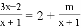 无解,则m的值为( )
无解,则m的值为( )
A. ﹣5 B. ﹣8 C. ﹣2 D. 5
 A
【解析】试题分析:去分母得:3x﹣2=2x+2+m,由分式方程无解,得到x+1=0,即x=﹣1,代入整式方程得:﹣5=﹣2+2+m,解得:m=﹣5,故选A.
A
【解析】试题分析:去分母得:3x﹣2=2x+2+m,由分式方程无解,得到x+1=0,即x=﹣1,代入整式方程得:﹣5=﹣2+2+m,解得:m=﹣5,故选A. 菱形以特殊的对称美而深受人们的喜爱,在生产生活中有着广泛的应用,小龙家里有一面长4.2m、宽2.8m的墙壁准备装修,现有如图甲所示的型号瓷砖,其形状是一块长30cm、宽20cm的矩形,中间白色部分为菱形,阴影部分为带淡蓝色花纹的全等的四个直角三角形,解答下列各问:

(1)小龙家里的墙壁最少要贴这种瓷砖多少块?
(2)全部贴满后,这面墙壁上有多少个有淡蓝色花纹的菱形?
 (1)196;(2)169
【解析】试题分析:(1)根据墙壁的长与宽以及矩形瓷砖的长与宽进行计算求出所需要贴的瓷砖的行数与列数,然后进行计算即可得解;
(2)根据(1)中结论即可求出淡蓝色花纹的菱形个数.
试题解析:
【解析】
(1)4.2m=420cm,2.8m=280cm,
∵420÷30=14,280÷20=14,
∴贴满墙壁需要14行14列瓷砖,
...
(1)196;(2)169
【解析】试题分析:(1)根据墙壁的长与宽以及矩形瓷砖的长与宽进行计算求出所需要贴的瓷砖的行数与列数,然后进行计算即可得解;
(2)根据(1)中结论即可求出淡蓝色花纹的菱形个数.
试题解析:
【解析】
(1)4.2m=420cm,2.8m=280cm,
∵420÷30=14,280÷20=14,
∴贴满墙壁需要14行14列瓷砖,
... 
