题目内容
如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
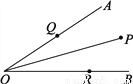
10cm
【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．
试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，
则PQ=EQ，PR=RF，
则△PQR的周长=PQ+QR+PR=EQ+QR+R...
练习册系列答案
相关题目
一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为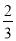
,应添加几个红球?
(1)不同意，理由见解析；（2）；（3）3.
【解析】试题分析：（1）求出分别摸到白球与摸到红球的概率，比较这两个概率，即可知道谁的可能性大，概率大则可能性就大；
（2）由（1）即可得出结论；
（3）此题考查了借助方程思想求概率的问题，解题的关键是找到等量关系．
试题解析：【解析】
（1）不同意，因为两种球数量不同，装有2个白球和1个红球，摸出白球的概率为，摸出红球的概率... 若ax＞b，ac2＜0，则x________．
＜
【解析】由ac2＜0，结合c2为正可知a＜0，
对ax＞b两边同时除以a，得x＜ .故答案为：＜. 在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.
126或66
【解析】试题分析：此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．
【解析】
当∠B为锐角时（如图1），
在Rt△ABD中，
BD===5cm，
在Rt△ADC中，
CD===16cm，
∴BC=21，
∴S△ABC==×21×12=126cm2；
当∠B为钝角... 由下列条件不能判定△ABC是直角三角形的是( )
A. ∠A＝37°，∠C＝53° B. ∠A－∠C＝∠B
C. ∠A∶∠B∶∠C＝3∶4∶5 D. ∠A∶∠B∶∠C＝2∶3∶5
C
【解析】解：A．∠B=180°－（37°+53°）=90°，是直角三角形；
B．∠B+∠C=∠A=180°－∠A，∴∠A=90°，是直角三角形；
C．∠C=180°×=75°，不是直角三角形；
D．∠C=180°×=90°，是直角三角形．
故选C． 如图，在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法)；
(2)在网格上的最小正方形的边长为1，求△ABC的面积．
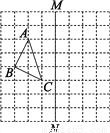
(1)见解析;（2）
【解析】试题分析：（1）根据网格特点分别找到A、B、C关于直线MN对称的点，然后顺次连接即可得；
（2）用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析：（1）如图所示：
（2）S△ABC＝2×3－2×(×1×2)－×1×3＝. 在“线段、锐角、三角形、等边三角形”这四个图形中，其中是轴对称图形的有___个，其中对称轴最多的是__________.
3 等边三角形
【解析】线段有两条对称轴，锐角有一条对称轴，等边三角形有三条对称轴，
故答案为：3，等边三角形． 如图所示，△ABC是不等边三角形，DE=BC，以D、E为两个顶点作位置不同的三角形，使所作三角形与△ABC全等，这样的三角形最多可以画出（ ）个．
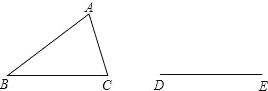
A．2 B．4 C．6 D．8
B.
【解析】
试题分析：可以做4个，分别是以D为圆心，AB为半径，作圆，以E为圆心，AC为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．然后以D为圆心，AC为半径，作圆，以E为圆心，AB为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．如图.
故选：B. 在Rt△ABC中，∠C＝90°，AC＝2，BC＝3，那么下列各式中，正确的是( )
A. sin B＝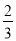
B. cos B＝
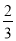C. tan B＝
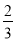D. tan B＝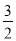
C
【解析】∵∠C＝90°，AC＝2，BC＝3，∴AB= ，
∴sinB= ，cosB=，tanB=，
故选C.