题目内容
若a－b＜0，则下列各式中一定正确的是（ ）
A、a＞b B、ab＞0 C、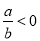
D、－a＞－b
D
【解析】
试题分析：由a－b＜0可得a＜b，再根据不等式的基本性质依次分析各项即可.
a－b＜0，
∴a＜b，
∴－a＞－b，但无法确定ab与的符号，
故选D.
练习册系列答案
相关题目
用计算器求tan35°的值，按键顺序是 ．
MODE，tan，35，=．
【解析】
试题分析：本题要求同学们能熟练应用计算器，会用科学记算器进行计算．
试题解析：根据已知一个角的正弦值求这个角的算法：先按MODE，选择模式；再键tan，35,最后按=；得到这个角的函数值． 将下列不等式的解集分别表示在数轴上：
(1)x≤2;
(2)x＞－2.
(1)见解析；（2）见解析
【解析】分析：根据不等式的解集在数轴上表示出来的方法画数轴即可，根据数轴的性质，实心圆点包括该点用“≥”，“≤”表示，空心圆圈不包括改点用“<”,“>”’表示，大于向右小于向左.
本题解析：
(1)
(2) 若ax＞b，ac2＜0，则x________．
＜
【解析】由ac2＜0，结合c2为正可知a＜0，
对ax＞b两边同时除以a，得x＜ .故答案为：＜. 有下列说法：
（1）若a＜b，则－a＞－b； （2）若xy＜0，则x＜0，y＜0；
（3）若x＜0，y＜0，则xy＜0； （4）若a＜b，则2a＜a＋b；
（5）若a＜b，则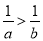
； （6）若
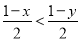，则x＞y.
其中正确的说法有（ ）
A、2个 B、3个 C、4个 D、5个
B
【解析】
试题分析：根据不等式的基本性质依次分析各项即可。
（1）若a＜b，则－a＞－b，正确；
（2）若xy＜0，则x＜0，y＞0或x＞0，y＜0，错误；
（3）若x＜0，y＜0，则xy＞0，错误；
（4）若a＜b，则2a＜a＋b，正确；
（5）若a＜0＜b，则，错误；
（6）若，则x＞y，正确.
故选B. 在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.
126或66
【解析】试题分析：此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．
【解析】
当∠B为锐角时（如图1），
在Rt△ABD中，
BD===5cm，
在Rt△ADC中，
CD===16cm，
∴BC=21，
∴S△ABC==×21×12=126cm2；
当∠B为钝角... 由下列条件不能判定△ABC是直角三角形的是( )
A. ∠A＝37°，∠C＝53° B. ∠A－∠C＝∠B
C. ∠A∶∠B∶∠C＝3∶4∶5 D. ∠A∶∠B∶∠C＝2∶3∶5
C
【解析】解：A．∠B=180°－（37°+53°）=90°，是直角三角形；
B．∠B+∠C=∠A=180°－∠A，∴∠A=90°，是直角三角形；
C．∠C=180°×=75°，不是直角三角形；
D．∠C=180°×=90°，是直角三角形．
故选C． 在“线段、锐角、三角形、等边三角形”这四个图形中，其中是轴对称图形的有___个，其中对称轴最多的是__________.
3 等边三角形
【解析】线段有两条对称轴，锐角有一条对称轴，等边三角形有三条对称轴，
故答案为：3，等边三角形． 一次函数的图象经过点(tan 45°，tan 60°)和(－cos 60°，－6tan 30°)，则此一次函数的表达式为________．
y＝2x－
【解析】tan 45°＝1，tan 60°＝，－cos 60°＝－，－6tan 30°＝－2，
设y＝kx＋b的图象经过点(1， )，（－ ，-2），
则有，解得： ，
∴一次函数解析式为： ，
故答案为： .