题目内容
11.使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是( )| A. | x<0 | B. | x<$\frac{1}{2}$ | C. | x$≥\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
分析 根据题意得出1-2x<0,进而求出答案.
解答 解:∵分式$\frac{{x}^{2}+1}{1-2x}$的值为负,
∴x的取值范围是:1-2x<0,
解得:x>$\frac{1}{2}$.
故选:D.
点评 此题主要考查了分式的值,得出1-2x的符号是解题关键.

练习册系列答案
相关题目
16.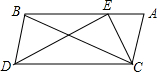 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )| A. | 107° | B. | 113° | C. | 115° | D. | 117° |
1.如果把分式$\frac{{a}^{2}}{a+b}$中的a和b都扩大n倍,那么分式的值( )
| A. | 扩大n倍 | B. | 不变 | C. | 扩大n2倍 | D. | 缩小为原来的$\frac{1}{n}$ |
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题: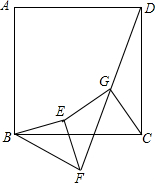 已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:
已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证: △ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?
△ABC内接于⊙O,∠B=60°,AC=2cm,⊙O的直径为多少?