题目内容
16．
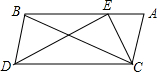如图，E为△ABC中AB边上一点，△ABC≌△EDC，∠ACE=46°，则∠DEB+∠BDC=（ ）| A． | 107° | B． | 113° | C． | 115° | D． | 117° |
分析 根据全等三角形的性质得到∠1=∠2，∠ACB=∠ECD，于是得到∠6=∠ACE=46°，根据三角形的内角和得到∠5=46°，根据等腰三角形的性质和三角形的内角和得到∠BDC=$\frac{1}{2}$（180°-∠6）=$\frac{1}{2}$（180°-46°）=67°，即可得到结论．
解答 
解：∵△ABC≌△EDC，
∴∠1=∠2，∠ACB=∠ECD，
∴∠6=∠ACE=46°，
∴∠3+∠4+∠2=134°，
∴∠1+∠3+∠4=134°，
∴∠5=46°，
∵BC=CD，
∴∠BDC=$\frac{1}{2}$（180°-∠6）=$\frac{1}{2}$（180°-46°）=67°，
∴∠DEB+∠BDC=113°．
故选B．
点评 本题考查了全等三角形的性质，三角形的内角和，等腰三角形的性质，熟练掌握等腰三角形的性质是解题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
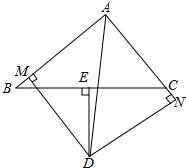如图，△ABC中，E是BC边上的中点，DE⊥BC于E，交∠BAC的平分线AD于D，过D点作DM⊥AB于M，作DN⊥AC于N，试证明：BM=CN．
11．使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是（ ）
| A． | x＜0 | B． | x＜$\frac{1}{2}$ | C． | x$≥\frac{1}{2}$ | D． | x$＞\frac{1}{2}$ |
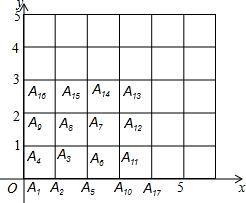如图所示，已知点A1的坐标为（0，0），点A2的坐标为（1，0），点A3的坐标为（1，1），点A4的坐标为（0，1），A5的坐标为（2，0），点A6坐标为（2，1），点A7的坐标为（2，2），点A8的坐标为（1，2），点A9的坐标为（0，2），点A10的坐标为（3，0），点A11的坐标为（3，1），…，依此规律排列下去，则点A25的坐标为（0，4），点A2015的坐标为（34，44）．
8．关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x（x-1）}$=0有解，则k满足（ ）
| A． | k≠-3 | B． | k≠5 | C． | k≠-3且k≠-5 | D． | k≠-3且k≠5 |
5．化简分式：$\frac{x-\frac{1}{y}}{y-\frac{1}{x}}$等于（ ）
| A． | 1 | B． | $\frac{y}{x}$ | C． | $\frac{x}{y}$ | D． | $\frac{x}{y}-\frac{y}{x}$ |