题目内容
1．如果把分式$\frac{{a}^{2}}{a+b}$中的a和b都扩大n倍，那么分式的值（ ）| A． | 扩大n倍 | B． | 不变 | C． | 扩大n2倍 | D． | 缩小为原来的$\frac{1}{n}$ |
分析 依题意分别用na和nb去代换原分式中的a和b，利用分式的基本性质化简即可．
解答 解：分别用na和nb去代换原分式中的a和b，得：
$\frac{（na）^{2}}{na+nb}=\frac{{n}^{2}{a}^{2}}{n（a+b）}=\frac{n{a}^{2}}{a+b}=n•\frac{{a}^{2}}{a+b}$，
故选：A．
点评 本题考查了分式的基本性质，解题的关键是抓住分子、分母变化的倍数，解此类题首先把字母变化后的值代入式子中，然后约分，再与原式比较，最终得出结论．
练习册系列答案
相关题目
11．使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是（ ）
| A． | x＜0 | B． | x＜$\frac{1}{2}$ | C． | x$≥\frac{1}{2}$ | D． | x$＞\frac{1}{2}$ |
如图，△ABC中，AB=AC，E、F、G分别是BC、AB、AC上一点，∠FEG=2∠B．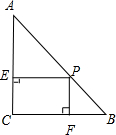
已知△ABC中，AC=BC=3$\sqrt{2}$，∠C=90°，AB上有一动点P，过点P作PE⊥AC于E，PF⊥BC于F．