题目内容
20.(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
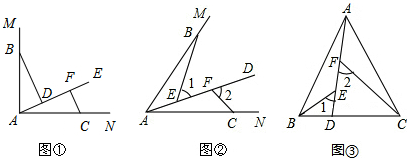
分析 图①,求出∠BDA=∠AFC=90°,∠ABD=∠CAF,根据AAS证两三角形全等即可;图②根据已知和三角形外角性质求出∠ABE=∠CAF,∠BAE=∠FCA,根据ASA证两三角形全等即可;图③求出△ABD的面积,根据△ABE≌△CAF得出△ACF与△BDE的面积之和等于△ABD的面积,即可得出答案.
解答 解:(1)如图①,
∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
$\left\{\begin{array}{l}{∠ADB=∠CFA}\\{∠ABD=∠CAF}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAF(AAS);
(2)∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
$\left\{\begin{array}{l}{∠ABE=∠CAF}\\{AB=AC}\\{∠BAE=∠ACF}\end{array}\right.$,
∴△ABE≌△CAF(ASA);
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是:$\frac{1}{3}$×15=5,
由(2)中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5.
点评 本题考查了全等三角形的性质和判定,三角形的面积,三角形的外角性质等知识点,主要考查学生的分析问题和解决问题的能力,题目比较典型,证明过程有类似之处.

练习册系列答案
相关题目
11.使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是( )
| A. | x<0 | B. | x<$\frac{1}{2}$ | C. | x$≥\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
8.关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x(x-1)}$=0有解,则k满足( )
| A. | k≠-3 | B. | k≠5 | C. | k≠-3且k≠-5 | D. | k≠-3且k≠5 |
5.化简分式:$\frac{x-\frac{1}{y}}{y-\frac{1}{x}}$等于( )
| A. | 1 | B. | $\frac{y}{x}$ | C. | $\frac{x}{y}$ | D. | $\frac{x}{y}-\frac{y}{x}$ |
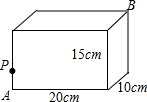 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少? 如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.
如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.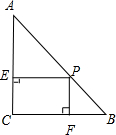 已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.
已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.