题目内容
4．计算（1）化简：（$\sqrt{15}$-3）0+2sin30°-$\root{3}{8}$-|-2|
（2）解方程：1+$\frac{3x}{x-2}$=$\frac{6}{2-x}$．
分析 （1）原式第一项利用零指数幂法则计算，第二项利用特殊角的三角函数值计算，第三项利用立方根定义计算，最后一项利用绝对值的代数意义化简，计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=1+1-2-2=-2；
（2）去分母得：x-2+3x=-6，
解得：x=-1，
经检验x=-1是分式方程的解．
点评 此题考查了实数的运算，以及解分式方程，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．若关于x的一元二次方程（m+1）x2-2x+1=0有实数根，则实数m的取值范围是（ ）
| A． | m≥0 | B． | m≤0 | C． | m≠1 | D． | m≤0且m≠-1 |
12．使得二次根式$\sqrt{3-4x}$有意义的字母x的取值范围是（ ）
| A． | x≥$\frac{3}{4}$ | B． | x≤$\frac{3}{4}$ | C． | x＜$\frac{3}{4}$ | D． | x≠$\frac{3}{4}$ |
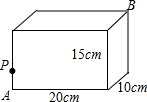如图，长方体的长为20cm，宽为10cm，高为15cm，棱上点P与顶点A相距5cm，一只蚂蚁如果要沿着长方体表面从点P爬到点B处，需要爬行的最短距离是多少？
11．使分式$\frac{{x}^{2}+1}{1-2x}$的值为负的x的取值范围是（ ）
| A． | x＜0 | B． | x＜$\frac{1}{2}$ | C． | x$≥\frac{1}{2}$ | D． | x$＞\frac{1}{2}$ |