题目内容
20. 【阅读理解】
【阅读理解】在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段中点坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$)
【运用知识解决问题]
(1)若点M(-1,2)、N(2013,2014)的中点为O,则点O的坐标是(1006,1008);若线段KH的中点坐标为(-2,3),且点K的坐标为(1,5),则点H的坐标是(-5,1)
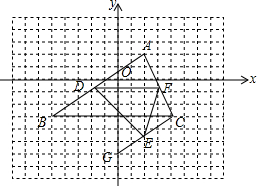
(2)如图,在平面直角坐标系中,三角形ABC的三个顶点坐标分别是A(2,2)、B(-5,-3)、C(4,3),点D、F分别是△三角形ABC的边AB、AC的中点,G(0,-6),E是线段CG的中点,求三角形DEF的面积.
分析 (1)根据中点坐标公式即可求出点O的坐标,先设点H的坐标为(m,n),根据中点公式列出方程求出m、n即可;
(2)根据中点公式分别求出点D、E、F的坐标,再求出三角形的底边DF的长及该边上的高,根据面积公式计算可得.
解答 解:(1)点O的坐标为:($\frac{-1+2013}{2}$,$\frac{2+2014}{2}$),即(1006,1008);
设点H的坐标为(m,n),则$\frac{m+1}{2}$=-2,$\frac{n+5}{2}$=3,
解得:m=-5,n=1,
故点H坐标为(5,-1);
(2)∵G(0,-6),A(2,2)、B(-5,-3)、C(4,-3),
∴AB中点D的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$),AC的中点F的坐标为(3,-$\frac{1}{2}$),CG的中点E的坐标为(2,-$\frac{9}{2}$),
则DF=3-(-$\frac{3}{2}$)=$\frac{9}{2}$,点E到DF的距离为:$\frac{9}{2}$-$\frac{1}{2}$=4,
故S△DEF=$\frac{1}{2}$×$\frac{9}{2}$×4=9;
故答案为:(1)(1006,1008),(5,-1).
点评 本题主要考查坐标与图形的性质,掌握三角形面积的求法是基本技能,运用线段中点公式求中点坐标是求三角形面积的关键.

练习册系列答案
相关题目
9.若代数式$\sqrt{2-x}+\sqrt{3x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥2 | B. | x≤$\frac{2}{3}$ | C. | $\frac{2}{3}≤x≤2$ | D. | $\frac{2}{3}<x<2$ |
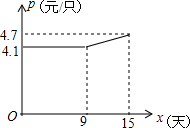 某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.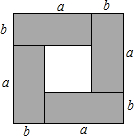 利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.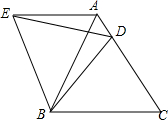 在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.
在等边三角形△ABC中,BC=6,点D是边AC上动点(点D与点A,C不重合),连接BD,将BD绕点B逆时针旋转60°得到BE,连接BD,AE.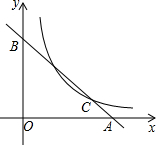 如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.
如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积. 如图,长方形的长与宽分别为a,b,它的周长为16,面积为10.求a2b+ab2的值.
如图,长方形的长与宽分别为a,b,它的周长为16,面积为10.求a2b+ab2的值.