题目内容
10.若$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$和$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$都是方程ax+by+2=0的解,请问$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$也是这个方程的解吗?说明理由.分析 将$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$和$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$代入方程ax+by+2=0,解关于a、b的二元一次方程组求得a、b的值,可得原方程,将x=4,y=4代入方程可知是否是方程的解.
解答 解:根据题意,得:$\left\{\begin{array}{l}{2a+3b+2=0}&{①}\\{-2a+b+2=0}&{②}\end{array}\right.$,
①+②,得:4b+4=0,
解得:b=-1,
将b=-1代入①,得:2a-3+2=0,
解得:a=$\frac{1}{2}$,
故原方程为:$\frac{1}{2}$x-y+2=0,
将x=4,y=4代入方程有:$\frac{1}{2}$×4-4+2=0,
故$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$也是这个方程的解.
点评 本题主要考查二元一次方程的解的概念及解二元一次方程组的能力,根据解的概念将x、y的值代入方程得到方程组是解题的前提,准确解方程组是解题的关键和基本能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
20.下列运算中正确的是( )
| A. | ${(\frac{1}{3})^{-2}}=-9$ | B. | (a-b)(-a-b)=a2-b2 | C. | 2a2•a3=2a6 | D. | (-a)10÷(-a)4=a6 |
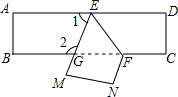
 如图所示,点D,A在直线AB上,点E,F在直线BC上,连接AC、DE、DF、AF.
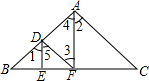
如图所示,点D,A在直线AB上,点E,F在直线BC上,连接AC、DE、DF、AF.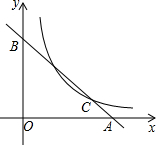 如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积.
如图,C是函数y=$\frac{8}{x}$(x>0)图象上的一个动点,过点C的直线CD分别交x轴,y轴于点A,B,且满足BC=2CA,求△AOB的面积. 如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.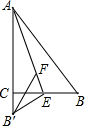 如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )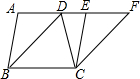 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.