题目内容
14.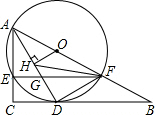 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
分析 (1)连接OD.先证明OD∥AC,得到∠CAD=∠ODA,再根据OA=OD,得到∠OAD=∠ODA,进而得到∠CAD=∠BAD,即可解答.
(2)①DF=DH,利用FH平分∠AFE,得到∠AFH=∠EFH,再证明∠DFH=∠DHF,即可得到DF=DH.
②设HG=x,则DH=DF=1+x,证明△DFG∽△DAF,得到$\frac{DF}{AD}=\frac{DG}{DF}$,即$\frac{1+x}{2(1+x)}=\frac{1}{1+x}$,求出x=1,再根据勾股定理求出AF,即可解答.
解答 解:(1)如图,连接OD,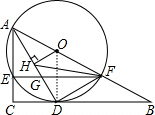
∵⊙O与BC相切于点D,
∴OD⊥BC,
∵∠C=90°,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠BAD,
∴AD平分∠CAB.
(2)①DF=DH,理由如下:
∵FH平分∠AFE,
∴∠AFH=∠EFH,
又∠DFG=∠EAD=∠HAF,
∴∠DFG=∠EAD=∠HAF,
∴∠DFG+∠GFH=∠HAF+∠HFA,
即∠DFH=∠DHF,
∴DF=DH.
②设HG=x,则DH=DF=1+x,
∵OH⊥AD,
∴AD=2DH=2(1+x),
∵∠DFG=∠DAF,∠FDG=∠FDG,
∴△DFG∽△DAF,
∴$\frac{DF}{AD}=\frac{DG}{DF}$,
∴$\frac{1+x}{2(1+x)}=\frac{1}{1+x}$,
∴x=1,
∵DF=2,AD=4,
∵AF为直径,
∴∠ADF=90°,
∴AF=$\sqrt{D{F}^{2}+A{D}^{2}}=\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$
∴⊙O的半径为$\sqrt{5}$.
点评 本题考查了切线的性质,相似三角形的判定和性质,本题涉及的知识点:两直线平行,等腰三角形的判定、三角形相似.

| 图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
| 平移 |  | (1)AB=A′B′,AB∥A′B′ | AA′=BB′ AA′∥BB′ |
| 轴对称 | 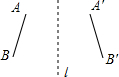 | (2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上. | (3)l垂直平分AA′ |
| 旋转 |  | AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. | (4)OA=OA′,∠AOA′=∠BOB′ |
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 3$\sqrt{3}$×2$\sqrt{2}$=6$\sqrt{5}$ | C. | 3$\sqrt{5}$÷$\frac{1}{{\sqrt{3}}}$×$\sqrt{3}$=3$\sqrt{5}$ | D. | 3÷$\sqrt{\frac{2}{3}}$=$\frac{3}{2}\sqrt{6}$ |
| 销售单价x(元/kg) | 120 | 130 | … | 180 |
| 每天销量y(kg) | 100 | 95 | … | 70 |
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
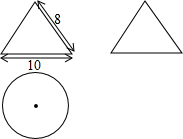 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
 如图,已知BC∥GE、AF∥DE、∠1=50°.
如图,已知BC∥GE、AF∥DE、∠1=50°.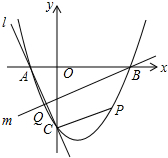 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)