题目内容
9.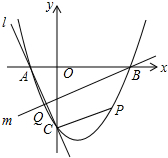 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
分析 (1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;
(2)连接BC,则△ABC的面积是不变的,过P作PM∥y轴,交BC于点M,设出P点坐标,可表示出PM的长,可知当PM取最大值时△PBC的面积最大,利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积;
(3)设直线m与y轴交于点N,交直线l于点G,由于∠AGP=∠GNC+∠GCN,所以当△AGB和△NGC相似时,必有∠AGB=∠CGB=90°,则可证得△AOC≌△NOB,可求得ON的长,可求出N点坐标,利用B、N两的点坐标可求得直线m的解析式.
解答 解:
(1)把B、C两点坐标代入抛物线解析式可得$\left\{\begin{array}{l}{9+3b+c=0}\\{c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴抛物线解析式为y=x2-2x-3;
(2)如图1,连接BC,过P作y轴的平行线,交BC于点M,交x轴于点H,
在y=x2-2x-3中,令y=0可得0=x2-2x-3,解得x=-1或x=3,
∴A点坐标为(-1,0),
∴AB=3-(-1)=4,且OC=3,
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×4×3=6,
∵B(3,0),C(0,-3),
∴直线BC解析式为y=x-3,
设P点坐标为(x,x2-2x-3),则M点坐标为(x,x-3),
∵P点在第四限,
∴PM=x-3-(x2-2x-3)=-x2+3x,
∴S△PBC=$\frac{1}{2}$PM•OH+$\frac{1}{2}$PM•HB=$\frac{1}{2}$PM•(OH+HB)=$\frac{1}{2}$PM•OB=$\frac{3}{2}$PM,
∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,
∵PM=-x2+3x=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴当x=$\frac{3}{2}$时,PMmax=$\frac{9}{4}$,则S△PBC=$\frac{3}{2}$×$\frac{9}{4}$=$\frac{27}{8}$,
此时P点坐标为($\frac{3}{2}$,-$\frac{15}{4}$),S四边形ABPC=S△ABC+S△PBC=6+$\frac{27}{8}$=$\frac{75}{8}$,
即当P点坐标为($\frac{3}{2}$,-$\frac{15}{4}$)时,四边形ABPC的面积最大,最大面积为$\frac{75}{8}$;
(3)①当点Q在x轴下方时,如图2,设直线m交y轴于点N,交直线l于点G,
则∠AGB=∠GNC+∠GCN,
当△AGB和△NGC相似时,必有∠AGB=∠CGB,
又∠AGB+∠CGB=180°,
∴∠AGB=∠CGB=90°,
∴∠ACO=∠OBN,
在Rt△AOC和Rt△NOB中
$\left\{\begin{array}{l}{∠AOC=∠NOB}\\{OC=OB}\\{∠ACO=∠NBO}\end{array}\right.$
∴Rt△AOC≌Rt△NOB(ASA),
∴ON=OA=1,
∴N点坐标为(0,-1),
设直线m解析式为y=kx+d,把B、N两点坐标代入可得$\left\{\begin{array}{l}{3k+d=0}\\{d=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{d=-1}\end{array}\right.$,
∴直线m解析式为y=$\frac{1}{3}$x-1;
②当点Q在x轴上方时,此时直线m与①中的直线m关于x轴对称,
∴解析式为y=-$\frac{1}{3}$x+1;
综上可知存在满足条件的直线m,其解析式为y=$\frac{1}{3}$x-1或y=-$\frac{1}{3}$x+1.
点评 本题为二次函数的综合应用,涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等.在(2)中确定出PM的值最大时四边形ABPC的面积最大是解题的关键,在(3)中确定出满足条件的直线m的位置是解题的关键.本题考查知识点较多,综合性较强,特别是第(2)问和第(3)问难度较大.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案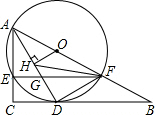 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G. 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: