题目内容
6.百子回归图是由1,2,3…,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四位“19 99 12 20”标示澳门回归日期,最后一行中间两位“23 50”标示澳门面积,…,同时它也是十阶幻方,其每行10个数之和,每列10个数之和,每条对角线10个数之和均相等,则这个和为505.
分析 根据已知得:百子回归图是由1,2,3…,100无重复排列而成,先计算总和;又因为一共有10行,且每行10个数之和均相等,所以每行10个数之和=总和÷10.
解答 解:1~100的总和为:$\frac{(1+100)×100}{2}$=5050,
一共有10行,且每行10个数之和均相等,所以每行10个数之和为:5050÷10=505,
故答案为:505.
点评 本题是数字变化类的规律题,是常考题型;一般思路为:按所描述的规律从1开始计算,从计算的过程中慢慢发现规律,总结出与每一次计算都符合的规律,就是最后的答案;此题非常简单,跟百子碑简介没关系,只考虑行、列就可以,同时,也可以利用列来计算.

练习册系列答案
相关题目
15.为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;
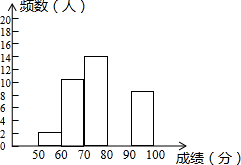
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 14 | b |
| 四 | 80≤x<90 | a | 0.32 |
| 五 | 90≤x<100 | 8 | 0.16 |
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
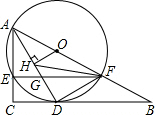 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G. 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: