题目内容
3.已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
分析 先求出A、B、C坐标,作CD⊥AB于D,根据tan∠ACD=$\frac{CD}{AD}$即可计算.
解答 解:令y=0,则-x2-2x+3=0,解得x=-3或1,不妨设A(-3,0),B(1,0),
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C(-1,4),
如图所示,作CD⊥AB于D.
在RT△ACD中,tan∠CAD=$\frac{CD}{AD}$=$\frac{4}{2}$=2,
故答案为D.
点评 本题考查二次函数与x轴交点坐标,锐角三角函数的定义,解题的关键是熟练掌握求抛物线与x轴交点坐标的方法,记住锐角三角函数的定义,属于中考常考题型.

练习册系列答案
相关题目
15.为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;
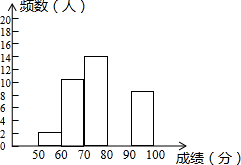
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 14 | b |
| 四 | 80≤x<90 | a | 0.32 |
| 五 | 90≤x<100 | 8 | 0.16 |
(1)本次决赛共有50名学生参加;
(2)直接写出表中a=16,b=0.28;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.
12. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.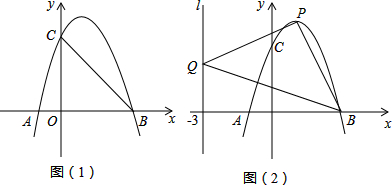
 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
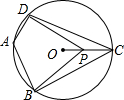 如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).
如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).