题目内容
19.一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:| 销售单价x(元/kg) | 120 | 130 | … | 180 |
| 每天销量y(kg) | 100 | 95 | … | 70 |
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
分析 (1)首先由表格可知:销售单价每涨10元,就少销售5kg,即可得y与x是一次函数关系,则可求得答案;
(2)首先设销售利润为w元,根据题意可得二次函数,然后求最值即可.
解答 解:(1)∵由表格可知:销售单价每涨10元,就少销售5kg,
∴y与x是一次函数关系,
∴y与x的函数关系式为:y=100-0.5(x-120)=-0.5x+160,
∵销售单价不低于120元/kg.且不高于180元/kg,
∴自变量x的取值范围为:120≤x≤180;
(2)设销售利润为w元,
则w=(x-80)(-0.5x+160)=-$\frac{1}{2}$x2+200x-12800=-$\frac{1}{2}$(x-200)2+7200,
∵a=-$\frac{1}{2}$<0,
∴当x<200时,w随x的增大而增大,
∴当x=180时,销售利润最大,最大利润是:w=-$\frac{1}{2}$(180-200)2+7200=7000(元),
答:当销售单价为180元时,销售利润最大,最大利润是7000元.
点评 此题考查了二次函数与一次函数的应用.注意理解题意,找到等量关系是关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
9. 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
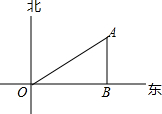 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )| A. | 250米 | B. | 250$\sqrt{3}$米 | C. | $\frac{500}{3}$$\sqrt{3}$米 | D. | 500$\sqrt{2}$米 |

 如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是4.
如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是4. 平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.