题目内容
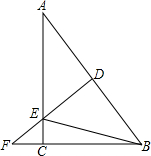 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.(1)求BE的长;
(2)求cos∠DFB的值.
考点:线段垂直平分线的性质,解直角三角形
专题:
分析:(1)根据题意可知,在Rt△ABC中,∠C=90°,AC=8,BC=6,根据勾股定理可得AB=10,AC=4,设BE为x,根据线段垂直平分线的性质可得AE=x,AD=BD=5,则CE=8-x,在Rt△CBE中,再一次使用勾股定理可解出x.即可求出BE的长;
(2)根据三角形内角和定理可得∠DFB=∠A,在Rt△ABC中利用余弦函数的定义求出cos∠A即可.
(2)根据三角形内角和定理可得∠DFB=∠A,在Rt△ABC中利用余弦函数的定义求出cos∠A即可.
解答:解:(1)在Rt△ABC中,∵∠C=90°,AC=8,BC=6,
∴AB=10.
设BE为x,
又∵DF是斜边AB的垂直平分线,分别交边AB、AC于点D、E,
∴AE=BE=x,AD=BD=5,
∴CE=8-x,
在Rt△BCE中,(8-x)2+62=x2,
解之x=
,
即BE=
;
(2)在Rt△CEF中,∵∠DFB+∠ECF+∠CEF=180°,
在Rt△ADE中,∵∠A+∠ADE+∠AED=180°,
又∵∠ECF=∠ADE=90°,∠CEF=∠AED,
∴∠DFB=∠A.
在Rt△ABC中,∵∠C=90°,
∴cos∠A=
=
=
.
∴AB=10.
设BE为x,
又∵DF是斜边AB的垂直平分线,分别交边AB、AC于点D、E,
∴AE=BE=x,AD=BD=5,
∴CE=8-x,
在Rt△BCE中,(8-x)2+62=x2,
解之x=
| 25 |
| 4 |
即BE=
| 25 |
| 4 |
(2)在Rt△CEF中,∵∠DFB+∠ECF+∠CEF=180°,
在Rt△ADE中,∵∠A+∠ADE+∠AED=180°,
又∵∠ECF=∠ADE=90°,∠CEF=∠AED,
∴∠DFB=∠A.
在Rt△ABC中,∵∠C=90°,
∴cos∠A=
| AC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
点评:此题主要考查了线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等.也考查了勾股定理,三角形内角和定理,锐角三角函数的定义.

练习册系列答案
相关题目
 如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数.
如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数. 如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.
如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.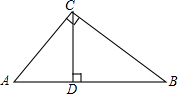 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:
 已知二次函数图象经过点(1,-3)、(-1,1)、(0,-2).
已知二次函数图象经过点(1,-3)、(-1,1)、(0,-2). 如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,H是EF的中点,求证:GH⊥EF.
如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,H是EF的中点,求证:GH⊥EF.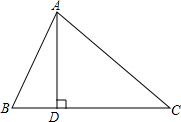 如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.
如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.