题目内容
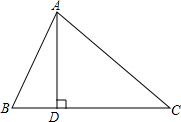 如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.
如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.(1)求AC的长;
(2)求S△ABC.
考点:勾股定理,含30度角的直角三角形,等腰直角三角形
专题:
分析:(1)在Rt△ABD中,根据AB=2cm,求出AD的长、BD的长;
(2)在△ABC中,利用三角形的面积公式解答.
(2)在△ABC中,利用三角形的面积公式解答.
解答:解:(1)在Rt△ABD中,AB=2cm,
AD=2sin60°=2×
=
cm,
BD=2cos60°=2×
=1cm,
在Rt△ADC中,CD=AD=
cm,
∴AC=
=
cm.
(2)在△ABC中,
BD+CD=(1+
)cm,
则(1+
)×
×
=
cm.
AD=2sin60°=2×
| ||
| 2 |
| 3 |
BD=2cos60°=2×
| 1 |
| 2 |
在Rt△ADC中,CD=AD=
| 3 |
∴AC=
(
|
| 6 |
(2)在△ABC中,
BD+CD=(1+
| 3 |
则(1+
| 3 |
| 3 |
| 1 |
| 2 |
3+
| ||
| 2 |
点评:本题考查了勾股定理、含30°角的直角三角形、等腰直角三角形,注意灵活运用各边之间的关系.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.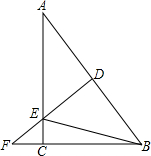 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.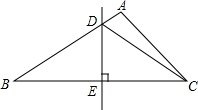 如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm.
如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm.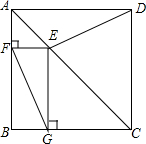 如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB.
如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB.