题目内容
如图，AB=AC，AD是∠EAC的平分线，AD∥BC，∠B=64°，求∠EAD、∠DAC、∠C的度数．考点：等腰三角形的性质,平行线的性质
专题：
分析：根据两直线平行，同位角相等求出∠EAD=∠B，再根据角平分线的定义可得∠DAC=∠EAD，然后利用两直线平行，内错角相等可得∠C=∠DAC．
解答：解：∵AD∥BC，∠B=64°，
∴∠EAD=∠B=64°，
∵AD是∠EAC的平分线，
∴∠DAC=∠EAD=64°，
又∵AD∥BC，
∴∠C=∠DAC=64°．
∴∠EAD=∠B=64°，
∵AD是∠EAC的平分线，
∴∠DAC=∠EAD=64°，
又∵AD∥BC，
∴∠C=∠DAC=64°．
点评：本题主要考查了平行线的性质，角平分线的定义，是基础题，熟记性质是解题的关键．
练习册系列答案
相关题目
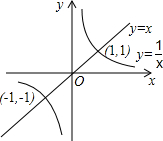我们知道，比较两个数的大小有很多方法，其中的图象法也非常巧妙．比如，通过图中的信息我们可以得出x＞| 1 |
| x |
| A、x＞1 |
| B、-1＜x＜0 |
| C、x＞1或-1＜x＜0 |
| D、以上都不对 |
求图中的三视图所表示的几何体的体积．
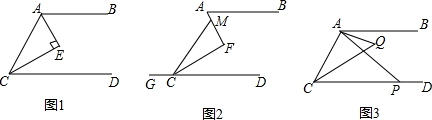
直线在AB、CD相交于点O，OE平分∠BOD，若∠AOD：∠DOE=7：1，求∠AOC的度数．
如图，某地有一座圆弧形的拱桥，圆弧所在圆的圆心为O，半径为OC，桥下水面宽AB为7.2m，拱顶C高出2.4m（CD=2.4m），现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船DFNM要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．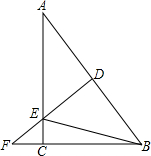
如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，DF是斜边AB的垂直平分线，分别交边AB、AC及BC的延长线于点D、E、F，连接BE．