题目内容
 如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.
如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.考点:平行四边形的性质
专题:
分析:由条件可证明△ABE∽△ADF,可求得AB:AD=2:3,且AB+AD=15,可求得AB和AD,在Rt△ABE中可求得AE,可求出四边形ABCD的面积.
解答:解:∵四边形ABCD为平行四边形,
∴∠B=∠D,AB=CD,AD=BC,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴AB:AD=AE:AF=2:3,
又∵四边形ABCD的周长为30cm,
∴AB+AD=15cm,
∴AB=6cm,AD=9cm,
又∵∠C=120°,
∴∠B=60°,
∴∠BAE=30°,
∴BE=
AB=3cm,
由勾股定理可求得AE=3
cm,
∴S四边形ABCD=BC•AE=9×3
=27
(cm2),
即四边形ABCD的面积为27
cm2.
∴∠B=∠D,AB=CD,AD=BC,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∴△ABE∽△ADF,
∴AB:AD=AE:AF=2:3,
又∵四边形ABCD的周长为30cm,
∴AB+AD=15cm,
∴AB=6cm,AD=9cm,
又∵∠C=120°,
∴∠B=60°,
∴∠BAE=30°,
∴BE=
| 1 |
| 2 |
由勾股定理可求得AE=3
| 3 |
∴S四边形ABCD=BC•AE=9×3
| 3 |
| 3 |
即四边形ABCD的面积为27
| 3 |
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
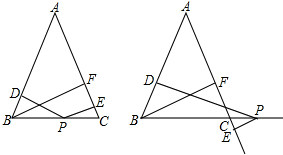
 直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.
直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数. 如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由. 如图所示的图形是一个物体的三视图,请画出这个物体的大致形状.
如图所示的图形是一个物体的三视图,请画出这个物体的大致形状.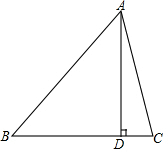 如图,在△ABC中,AD⊥BC于点D,AB=2
如图,在△ABC中,AD⊥BC于点D,AB=2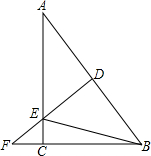 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.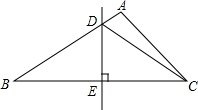 如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm.
如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm.