题目内容
 如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,H是EF的中点,求证:GH⊥EF.
如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,H是EF的中点,求证:GH⊥EF.考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:连接GF,可证明△GEF为等腰三角形,结合条件可证明GH⊥EF.
解答: 证明:
证明:
如图,连接GF,
∵G、F分别为AC、CD的中点,
∴GF是△ACD的中位线,
∴GF=
AD,
同理可得GE=
BC,
又AD=BC,
∴GF=GE,
∵H为EF的中点,
∴GH⊥EF.
 证明:
证明:如图,连接GF,
∵G、F分别为AC、CD的中点,
∴GF是△ACD的中位线,
∴GF=
| 1 |
| 2 |
同理可得GE=
| 1 |
| 2 |
又AD=BC,
∴GF=GE,
∵H为EF的中点,
∴GH⊥EF.
点评:本题主要考查三角形中位线定理和等腰三角形的性质,由中位线定理证得△GEF为等腰三角形是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.
直线在AB、CD相交于点O,OE平分∠BOD,若∠AOD:∠DOE=7:1,求∠AOC的度数.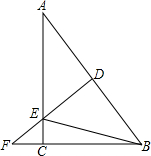 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE. 画出y=x+0.5的函数图象.
画出y=x+0.5的函数图象.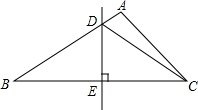 如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm.
如图,已知△ABC中,AB比AC长5cm,BC的垂直平分线叫AB于D,交BC于E,△ACD的周长是25cm. 如图,一根49厘米长的绳子的两端钉在A、B两点,AB=7厘米,提拉绳子到点P,使PA⊥AB,此时绳子绷紧,则PB=
如图,一根49厘米长的绳子的两端钉在A、B两点,AB=7厘米,提拉绳子到点P,使PA⊥AB,此时绳子绷紧,则PB=