题目内容
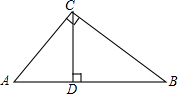如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，设AC=b，BC=a，AB=c，CD=h．求证：（1）
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
（2）a+b＜c+h；
（3）以a+b，h，c+h为边的三角形是直角三角形．
考点：勾股定理,勾股定理的逆定理
专题：证明题
分析：（1）要证明
+
=
，只需证h2（
+
）=1即可，在直角△ABC中根据BD2+CD2=BC2求证．
（2）根据三角形的面积公式求出ab=ch，利用勾股定理可得a2+b2=c2，再利用完全平方公式整理即可得证；
（3）先分别求出（a+b）2，h2，（c+h）2的值，再根据勾股定理的逆定理进行判断即可．
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
（2）根据三角形的面积公式求出ab=ch，利用勾股定理可得a2+b2=c2，再利用完全平方公式整理即可得证；
（3）先分别求出（a+b）2，h2，（c+h）2的值，再根据勾股定理的逆定理进行判断即可．
解答：证明：（1）在直角△ABC中，∠ACB=90°，CD⊥AB，则△ACB∽△ADC∽△CDB，
=
，即
=
，
∵h2（
+
）=
+
=
+
=
=1，
∴
+
=
；
（2）∵CD⊥AB，∠ACB=90°，
∴S△ABC=
ab=
ch，
∴ab=ch，
∵∠ACB=90°，
∴a2+b2=c2，
∴（a+b）2=a2+2ab+b2=c2+2ch，（c+h）2=c2+2ch+h2，
∵a、b、c、h都是正数，
∴（a+b）2＜（c+h）2，
∴a+b＜c+h；
（3）∵（c+h）2=c2+2ch+h2；
h2+（a+b）2=h2+a2+2ab+b2，a2+b2=c2（勾股定理），ab=ch（面积公式推导），
∴c2+2ch+h2=h2+a2+2ab+b2，
∴（c+h）2=h2+（a+b）2，
∴根据勾股定理的逆定理知道以h，c+h，a+b为边构成的三角形是直角三角形．
| CD |
| AC |
| BD |
| BC |
| CD2 |
| AC2 |
| BD2 |
| BC2 |
∵h2（
| 1 |
| a2 |
| 1 |
| b2 |
| CD2 |
| BC2 |
| CD2 |
| AC2 |
| CD2 |
| BC2 |
| BD2 |
| BC2 |
| BC2 |
| BC2 |
∴
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
（2）∵CD⊥AB，∠ACB=90°，
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴ab=ch，
∵∠ACB=90°，
∴a2+b2=c2，
∴（a+b）2=a2+2ab+b2=c2+2ch，（c+h）2=c2+2ch+h2，
∵a、b、c、h都是正数，
∴（a+b）2＜（c+h）2，
∴a+b＜c+h；
（3）∵（c+h）2=c2+2ch+h2；
h2+（a+b）2=h2+a2+2ab+b2，a2+b2=c2（勾股定理），ab=ch（面积公式推导），
∴c2+2ch+h2=h2+a2+2ab+b2，
∴（c+h）2=h2+（a+b）2，
∴根据勾股定理的逆定理知道以h，c+h，a+b为边构成的三角形是直角三角形．
点评：本题考查的是勾股定理的逆定理及三角形的面积公式，熟知勾股定理的逆定理是解答此题的关键．
练习册系列答案
相关题目
求图中的三视图所表示的几何体的体积．
如图，某地有一座圆弧形的拱桥，圆弧所在圆的圆心为O，半径为OC，桥下水面宽AB为7.2m，拱顶C高出2.4m（CD=2.4m），现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船DFNM要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．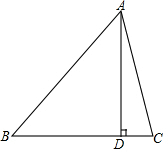
如图，在△ABC中，AD⊥BC于点D，AB=2
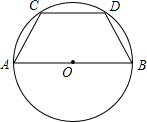如图，AB为⊙O的直径，C，D是半圆上两点，且AC=CD=DB，AB=10cm
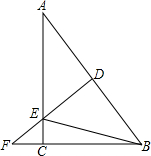如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，DF是斜边AB的垂直平分线，分别交边AB、AC及BC的延长线于点D、E、F，连接BE．
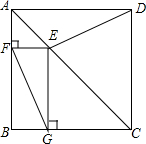如图，四边形ABCD是正方形，点E是AC上的点EG⊥BC，EF⊥AB．