题目内容
(1)如图①,若AD⊥BD,AE⊥CE,且BD,CE分别平分△ABC的两个外角,试探索线段DE与△ABC的三条边AB、BC、AC之间的关系,并说明理由;
(2)如图②,若DB、CE是△ABC的两个内角平分线,(1)中的结论是否仍成立?如果成立,说明理由;如果不成立,试写出所包含的结论.

(2)如图②,若DB、CE是△ABC的两个内角平分线,(1)中的结论是否仍成立?如果成立,说明理由;如果不成立,试写出所包含的结论.

考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:(1)延长AD交CB延长线于点G,延长AE交BC的延长线于点H,由条件可证明AB=BG,AC=CH,结合中位线定理可得出DE=
GH,可找到DE与AB、BC、AC之间的关系;
(2)结论不成立,同样的方法可找到DE与AB、AC、BC之间的关系.
| 1 |
| 2 |
(2)结论不成立,同样的方法可找到DE与AB、AC、BC之间的关系.
解答:解:(1)DE=
(AB+AC+BC),理由如下:
如图1,延长AD交CB延长线于点G,延长AE交BC的延长线于点H,
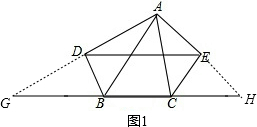
∵BD平分∠ABG,AD⊥BD,
∴BA=BG,同理AC=CH,
∴D、E分别为AG、AH的中点,
∴DE为△AGH的中位线,
∴DE=
GH,
又∵GH=GB+BC+CH=AB+BC+AC,
∴DE=
(AB+BC+AC);
(2)不成立,此时DE=
(AB+AC-BC),理由如下:
如图2,延长AE交BC于点G,延长AD交BC于点H,
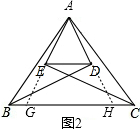
同(1)的方法可得到BH=AB,CG=AC,且DE=
GH,
∴DE=
(AB+AC-BC).
| 1 |
| 2 |
如图1,延长AD交CB延长线于点G,延长AE交BC的延长线于点H,

∵BD平分∠ABG,AD⊥BD,
∴BA=BG,同理AC=CH,
∴D、E分别为AG、AH的中点,
∴DE为△AGH的中位线,
∴DE=
| 1 |
| 2 |
又∵GH=GB+BC+CH=AB+BC+AC,
∴DE=
| 1 |
| 2 |
(2)不成立,此时DE=
| 1 |
| 2 |
如图2,延长AE交BC于点G,延长AD交BC于点H,

同(1)的方法可得到BH=AB,CG=AC,且DE=
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
点评:本题主要考查等腰三角形的判定和性质及三角形中位线定理,由条件构造等腰三角形再利用三角形中位线定理找到DE与AB、AC、BC的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知(2x-1)4=a1x4+a2x3+a3x2+a4x+a5,则a1-a2+a3-a4+a5-1的值为( )
| A、0 | B、-13 | C、-82 | D、80 |
 如图所示的图形是一个物体的三视图,请画出这个物体的大致形状.
如图所示的图形是一个物体的三视图,请画出这个物体的大致形状.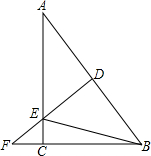 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,DF是斜边AB的垂直平分线,分别交边AB、AC及BC的延长线于点D、E、F,连接BE. 画出y=x+0.5的函数图象.
画出y=x+0.5的函数图象.