题目内容
10. 如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
分析 连接OB和AC交于点Q,关键平行四边形的性质求得Q(2,2),即可判定Q在反比例函数y=$\frac{4}{x}$的图象上,作出直线y=-x+4即可判定S1>S2.
解答 解;连接OB和AC交于点Q,
∵四边形ABCD为平行四边形,B(4,4),
∴点Q的坐标为(2,2),
∴点Q在反比例函数y=$\frac{4}{x}$的图象上,
作出直线y=-x+4,可知直线经过Q点,因此平行四边形被直线分成的两部分的面积相等,
∴S1>S2,
故答案为S1>S2.
点评 本题考查了反比例函数系数k的几何意义以及平行四边形的性质,判定D、E关于平行四边形对角线的交点对称是解题的关键.

练习册系列答案
相关题目
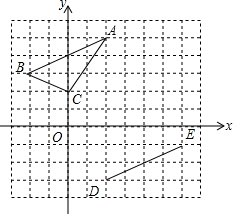 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).
在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).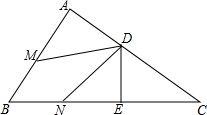 如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.
如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.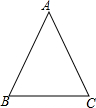 如图,等腰△ABC中,AB=AC.
如图,等腰△ABC中,AB=AC.