题目内容
19.解不等式组:(1)$\left\{\begin{array}{l}{2x>1-x}\\{x+2<4x-1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-5<1+2x}\\{3x+2≤4x}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x}\\{x-1≤\frac{3}{4}x-\frac{1}{8}}\end{array}\right.$
(4)$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}-1<2-x}\end{array}\right.$.
分析 (1)求出两不等式的解集,根据:“同大取大”确定不等式组解集;
(2)求出两不等式的解集,根据:“同大取大”确定不等式组解集;
(3)求出两不等式的解集,根据:“大小小大中间找”确定不等式组解集;
(4)求出两不等式的解集,根据:“同大大小小无解了”确定不等式组解集.
解答 解:(1)解不等式2x>1-x,得:x>$\frac{1}{3}$,
解不等式x+2<4x-1,得:x>1,
故不等式组的解集为:x>1;
(2)解不等式x-5<1+2x,得:x>-6,
解不等式3x+2≤4x,得:x≥2,
故不等式组的解集为:x≥2;
(3)解不等式$\frac{2}{3}$x+5>1-x,得:x>-$\frac{12}{5}$,
解不等x-1≤$\frac{3}{4}$x-$\frac{1}{8}$,得:x≤$\frac{7}{2}$,
故不等式组的解集为:-$\frac{12}{5}$<x$≤\frac{7}{2}$;
(4)解不等式2x+3≥x+11,得:x≥8,
解不等式$\frac{2x+5}{3}$-1<2-x,得:x<-$\frac{4}{5}$,
故不等式组无解.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3). 如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2. 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于A,B两点,与y轴相交于C点且OA=OC,对称轴为x=1,有下列结论:①2a+b=0;②ac+b+1=0;③0<a<$\frac{1}{2}$;④当m≠1时,a+b>am2+bm,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于A,B两点,与y轴相交于C点且OA=OC,对称轴为x=1,有下列结论:①2a+b=0;②ac+b+1=0;③0<a<$\frac{1}{2}$;④当m≠1时,a+b>am2+bm,其中正确结论的个数是( )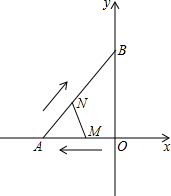 如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0). 有理数a,b,c在数轴上对应的点的位置如图所示,化简|a|+|a+b|+|b-c|+|b+c-a|的结果是a-3b.
有理数a,b,c在数轴上对应的点的位置如图所示,化简|a|+|a+b|+|b-c|+|b+c-a|的结果是a-3b.