题目内容
2.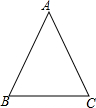 如图,等腰△ABC中,AB=AC.
如图,等腰△ABC中,AB=AC.(1)操作(保留作图痕迹,不写作法);
①以CA为直径作⊙O,交AB于M,交BC于N.
②过C点作⊙O的切线交AB的延长线于点P;
(2)在(1)中要求所作的图中,若BC=10,AC=13,求PC•AM的值.
分析 (1)作AC的垂直平分线得到AC的中点O,再以O点为圆心,OA为半径作圆交AB于M,交BC于N;然后过点C作PC⊥AC于C,交AB的延长线于点P,则PC为切线;
(2)连结AN、CM,如图,根据圆周角定理得到∠AMC=∠ANC=90°,则利用等腰三角形的性质得NB=NC=$\frac{1}{2}$BC=5,利用勾股定理可计算出AN=12,再利用面积法计算出CM=$\frac{120}{13}$,接着根据切线的性质得∠ACP=90°,然后证明Rt△AMC∽Rt△ACP后利用相似比可计算出PC•AM的值.
解答 解:(1)如图⊙O和切线PC为所作;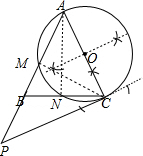
(2)连结AN、CM,如图,
∵CA为直径,
∴∠AMC=∠ANC=90°,
∵AB=AC,
∴NB=NC=$\frac{1}{2}$BC=5,
在Rt△ACN中,AN=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∵$\frac{1}{2}$CM•AB=$\frac{1}{2}$•AN•BC,
∴CM=$\frac{12×10}{13}$=$\frac{120}{13}$,
∵PC为切线,
∴AC⊥PC,
∴∠ACP=90°,
∵∠MAC=∠CAP,
∴Rt△AMC∽Rt△ACP,
∴CM:PC=AM:AC,即$\frac{120}{13}$:PC=AM:13,
∴PC•AM=$\frac{120}{13}$×13=120.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解决(2)小题的关键是证明Rt△AMC∽Rt△ACP后利用相似比求PC•AM的值.

练习册系列答案
相关题目
12.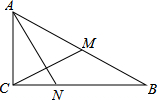 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
13.中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中12.6万用科学记数法表示应为( )
| A. | 1.26×106 | B. | 12.6×104 | C. | 1.26×105 | D. | 0.126×106 |
 如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.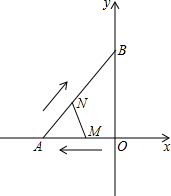 如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).