题目内容
11．$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$+$\frac{1}{\sqrt{101}+\sqrt{100}}$=$\sqrt{101}$-1．分析 先分母有理化，再合并同类二次根式即可．
解答 解：原式=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）×（\sqrt{2}-1）}$+$\frac{1×（\sqrt{3}-\sqrt{2}）}{（\sqrt{3}+\sqrt{2}）×（\sqrt{3}-\sqrt{2}）}$+$\frac{1×（\sqrt{4}-\sqrt{3}）}{（\sqrt{4}+\sqrt{3}）×（\sqrt{4}-\sqrt{3}）}$+…+$\frac{1×（\sqrt{101}-\sqrt{100}）}{（\sqrt{101}+\sqrt{100}）×（\sqrt{101}-\sqrt{100}）}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{101}$-$\sqrt{100}$
=$\sqrt{101}$-1，
故答案为：$\sqrt{101}$-1．
点评 本题考查了分母有理化的应用，能正确分母有理化是解此题的关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
如图，在平面直角坐标系中，?ABCO的顶点A在x轴上，顶点B的坐标为（4，4），反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分，其面积分别为S1、S2，则S1、S2的大小关系为S1＞S2．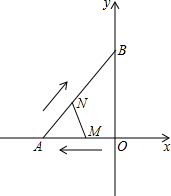
如图，在平面直角坐标系中，Rt△AOB的顶点A，B分别落在坐标轴上，O为原点，点A的坐标为（-12，0），点B坐标为（0，16），动点M从点O出发．沿OA向中点A以每秒2个单位的速度运动，同时动点N从A出发，沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动，当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．
有理数a，b，c在数轴上对应的点的位置如图所示，化简|a|+|a+b|+|b-c|+|b+c-a|的结果是a-3b．