题目内容
20.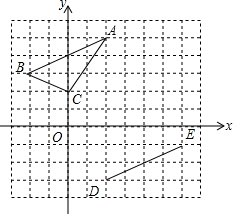 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).
在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).(1)线段AB先向右平移4个单位,再向下平移6个单位与线段ED重合;
(2)将△ABC绕点P旋转180°后得到的△DEF,使AB的对应边为DE,直接写出点P的坐标,并画出△DEF;
(3)求点C在旋转过程中所经过的路径l的长.
分析 (1)直接利用平移的性质得出平移规律即可;
(2)利用旋转的性质得出对应点位置进而得出答案;
(3)利用弧长公式进而求出答案.
解答  解:(1)AB先向右平移4个单位,再向下平移6个单位与ED重合;
解:(1)AB先向右平移4个单位,再向下平移6个单位与ED重合;
故答案为:右,4,下,6;
(2)如图所示:P(2,1),画出△DEF;
(3)点C在旋转过程中所经过的路径长l=$\sqrt{5}π$.
点评 此题主要考查了旋转变换和平移变换,正确得出对应点位置是解题关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
10.设a是方程x2+2x-2=0的一个实数根,则2a2+4a+2016的值为( )
| A. | 2016 | B. | 2018 | C. | 2020 | D. | 2021 |
15.在-3、0、4、0.5这四个数中最小的数是( )
| A. | -3 | B. | 0.5 | C. | 0 | D. | 4 |
12.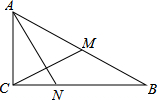 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3). 如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.