题目内容
5.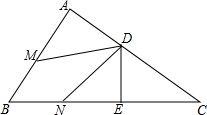 如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.
如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.
分析 连接BD,先证明△BDM≌△BDN得∠DBM=∠DBN,根据角平分线性质定理即可证明.
解答 证明:连接BD.
在△BDM和△BDN中,
$\left\{\begin{array}{l}{BM=BN}\\{BD=BD}\\{DDN}\end{array}\right.$,
∴△BDM≌△BDN,
∴∠DBM=∠DBN,
∵∠A=90°,
∴DA⊥BA,DE⊥BC,
∴DA=DE.
点评 本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会条件常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
15.在-3、0、4、0.5这四个数中最小的数是( )
| A. | -3 | B. | 0.5 | C. | 0 | D. | 4 |
13.中国移动数据中心IDC项目近日在高新区正式开工建设,该项目规划建设规模12.6万平方米,建成后将成为山东省最大的数据业务中心.其中12.6万用科学记数法表示应为( )
| A. | 1.26×106 | B. | 12.6×104 | C. | 1.26×105 | D. | 0.126×106 |
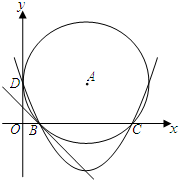 如图,在直角坐标系中,圆A与x轴交于点B、C,与y轴相切于点D,抛物线y=$\frac{1}{4}{x^2}-\frac{5}{2}$x+4经过B、C、D三点.
如图,在直角坐标系中,圆A与x轴交于点B、C,与y轴相切于点D,抛物线y=$\frac{1}{4}{x^2}-\frac{5}{2}$x+4经过B、C、D三点. 如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.
如图,在平面直角坐标系中,?ABCO的顶点A在x轴上,顶点B的坐标为(4,4),反比例函数y=$\frac{4}{x}$在第一象限的图象将?ABCO分割成两部分,其面积分别为S1、S2,则S1、S2的大小关系为S1>S2.