Question

5．如图，已知在△ABC中，AB=AC=10，tan∠B=$\frac{4}{3}$．
（1）求BC的长；
（2）点D在边AB上，且AD=1，M为边BC上一动点，连接DM．当△BDM是直角三角形时，求BM的长．

Answer 1

分析 （1）如图1过A作AD⊥BC于D，根据等腰三角形的性质得到BD=CD，解直角三角形即可得到结论；
（2）若∠BMD=90°，过A作AE⊥BC于E，列比例式即可得到BM=5.4，如图3，若∠BDM=90°，过A作AE⊥BC于E，根据相似三角形的性质得到BM=15，于是得到结论．

解答 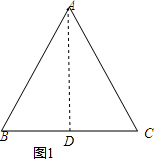解：（1）如图1过A作AD⊥BC于D，
∵AB=AC，
∴BD=CD，
∵tan∠B=$\frac{AD}{BD}$=$\frac{4}{3}$，
∴AD=$\frac{4}{3}$BD，
∵AD²+BD²=AB²，
∴（$\frac{4}{3}$BD）²+BD²=10²，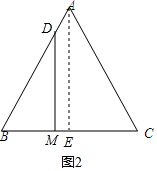
∴BD=6，
∴BC=12；
（2）若∠BMD=90°，过A作AE⊥BC于E，
则DM∥AE，
∴$\frac{BD}{AB}$=$\frac{BM}{BE}$，即$\frac{10-1}{10}$=$\frac{BM}{6}$，
∴BM=5.4，
如图3，若∠BDM=90°，过A作AE⊥BC于E，
∵∠BDM=∠AEB=90°，∠B=∠B，
∴△ABE∽△MBD，
∴$\frac{BM}{AB}=\frac{BD}{BE}$，即$\frac{BM}{10}=\frac{9}{6}$，
∴BM=15，
∵15＞12，∴BM=15应舍去，
故BM=5.4．

点评 本题考查了解直角三角形，等腰三角形的性质，相似三角形的判定和性质，正确的作出辅助线是解题的关键．