题目内容
14.若关于x的一元二次方程x2+4x-k=0有实数根,则k的最小值为-4.分析 根据判别式的意义得到△=42-4(-k)≥0,然后解不等式确定k的范围,再找出k的最小值即可.
解答 解:根据题意得△=42-4(-k)≥0,
解得k≥-4,
所以k的最小值为-4.
故答案为-4.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
4.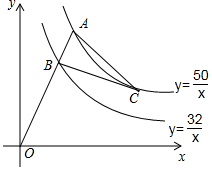 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{3}}{13}$ |
6.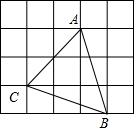 如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )
如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )
 如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )
如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{4}{5}$ |
3.2015年榕城区从中随机调查了5所初中九年级学生的数学考试成绩,学生的考试成绩情况如表(数学考试满分120分)
(1)这5所初中九年级学生的总人数有多少人?
(2)统计时,老师漏填了表中空白处的数据,请你帮老师填上;
(3)从这5所初中九年级学生中随机抽取一人,恰好是108分以上(不包括108分)的概率是多少?
| 分数段 | 频数 | 频率 |
| 72分以下 | 368 | 0.2 |
| 72----80分 | 460 | 0.25 |
| 81----95分 | 644 | 0.35 |
| 96----108分 | 184 | 0.2 |
| 109----119分 | 130 | |
| 120分 | 54 |
(2)统计时,老师漏填了表中空白处的数据,请你帮老师填上;
(3)从这5所初中九年级学生中随机抽取一人,恰好是108分以上(不包括108分)的概率是多少?
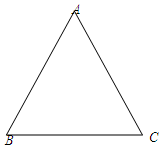 如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.
如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.
 如图,矩形OABC中,OA=3,OC=5,OA,OC分别在x轴,y轴上,D是边CB上的一个动点(不与C,B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.
如图,矩形OABC中,OA=3,OC=5,OA,OC分别在x轴,y轴上,D是边CB上的一个动点(不与C,B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.