题目内容
10.我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1,若我们规定一个新数i,使其满足i2=-1(即x2=-1方程有一个根为i),并且进一步规定:一切实数可以与新数进行四则运算,且原有的运算法则仍然成立,于是有i1=i,i2=-1,i3=i2•i=(-1)•i,i4=(i2)2=(-1)2=1,从而对任意正整数n,我们可得到i4n+1=i4n•i=(i4)n•i,同理可得i4n+2=-1,i4n+3=-i,i4n=1,那么,i+i2+i3+i4+…+i2016+i2017的值为( )| A. | 0 | B. | 1 | C. | -1 | D. | i |
分析 i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,i5=i4•i=i,i6=i5•i=-1,从而可得4次一循环,一个循环内的和为0,计算即可.
解答 解:由题意得,i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,i5=i4•i=i,i6=i5•i=-1,
故可发现4次一循环,一个循环内的和为0,
∵$\frac{2017}{4}$=504…1,
∴i+i2+i3+i4+…+i2013+i2017=i,
故选:D.
点评 本题考查了规律型:数字的变化类,实数的运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若函数y=(3m-2)x2+(1-2m)x是一次函数,则m的值是( )
| A. | m>$\frac{2}{3}$ | B. | m<$\frac{1}{2}$ | C. | m=$\frac{2}{3}$ | D. | m=$\frac{1}{2}$ |
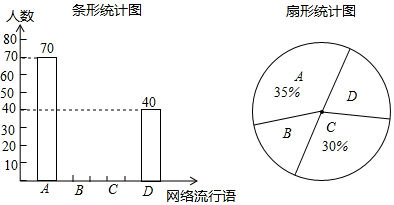
18. 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)m=10,n=60,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约为600万人,请你估计其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请结合上面的统计情况,用简短的语言发出倡议.
 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 20 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 80 |
| E | 其他 | 30 |
(1)m=10,n=60,扇形统计图中E组所占的百分比为15%;
(2)若该市人口约为600万人,请你估计其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请结合上面的统计情况,用简短的语言发出倡议.
15.下列实数中,有理数是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101001 |
 如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.
如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.