题目内容
 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°.(1)求作一点P,使得点P到B、C两点的距离相等,并且点P到AB、BC的距离也相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若∠ACP=15°,求∠ABP的度数.
考点:作图—复杂作图,角平分线的性质,线段垂直平分线的性质
专题:
分析:(1)利用中垂线到线段端点的距离相等及角平分线到两边的距离相等的性质作图即可.
(2)由中垂线到线段端点的距离相等及角平分线上的点到角的两边的距离相等的性质,可得出∠ABP=∠PBC=∠PCB,再利用∠ABP+∠PBC+∠PCB=120°求解即可.
(2)由中垂线到线段端点的距离相等及角平分线上的点到角的两边的距离相等的性质,可得出∠ABP=∠PBC=∠PCB,再利用∠ABP+∠PBC+∠PCB=120°求解即可.
解答:解:(1)如图,

(2)如图,

∵PD是BC的中垂线,
∴∠PBC=∠PCB,
∵BP是∠ABC的角平分线,
∴∠PBC=∠ABP,
∵∠A=60°,
∴∠ABP+∠PBC+∠PCB+∠ACP=120°,
∵∠ACP=15°,
∴∠ABP=35°.

(2)如图,

∵PD是BC的中垂线,
∴∠PBC=∠PCB,
∵BP是∠ABC的角平分线,
∴∠PBC=∠ABP,
∵∠A=60°,
∴∠ABP+∠PBC+∠PCB+∠ACP=120°,
∵∠ACP=15°,
∴∠ABP=35°.
点评:本题主要考查了作图,角平分线及中垂线的性质,解题的关键是熟记角平分线及中垂线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,AE的长度可表示为( )


| A、3(a-b) | B、3a-b |
| C、2a | D、2a+b |
 如图,直线AB,CD,EF相交于点O,∠AOE=24°,∠BOC=3∠AOC,求∠DOF的度数.
如图,直线AB,CD,EF相交于点O,∠AOE=24°,∠BOC=3∠AOC,求∠DOF的度数. 如图,直线AB,CD相交于点O,∠EOA=90°,∠COE=
如图,直线AB,CD相交于点O,∠EOA=90°,∠COE= 如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.
如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H. 如图,在△ABC中,AB=AC.BD平分∠ABC交AC于点D,若BD=BC,则∠A等于多少度?
如图,在△ABC中,AB=AC.BD平分∠ABC交AC于点D,若BD=BC,则∠A等于多少度?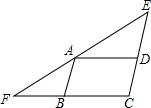 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b. 如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为
如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为