题目内容
已知抛物线y=x2+(m+1)x+m在x轴上截得的线段长为2,则m= .
考点:抛物线与x轴的交点
专题:
分析:令x2+(m+1)x+m=0,然后利用根与系数的关系,求出它的两根之积和两根之和,代入数轴上两点间的距离公式,列方程解答即可.
解答:解:令x2+(m+1)x+m=0
设方程的两个根为x1,x2
则x1+x2=-(m+1),x1•x2=m
∴|x1-x2|=
=2
∴(m+1)2-4m=4
整理得:m2-2m-3=0
解得:m1=-1,m2=3.
设方程的两个根为x1,x2
则x1+x2=-(m+1),x1•x2=m
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
∴(m+1)2-4m=4
整理得:m2-2m-3=0
解得:m1=-1,m2=3.
点评:本题考查二次函数的解析式和一元二次方程与二次函数的关系,函数与x轴的交点的横坐标就是方程的根.另外解答本题的关键是熟悉数轴上两点间的距离公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1)小英从家向( )走到小红家,也可以向( )走到超市,( )走到小红家;
(1)小英从家向( )走到小红家,也可以向( )走到超市,( )走到小红家; 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°.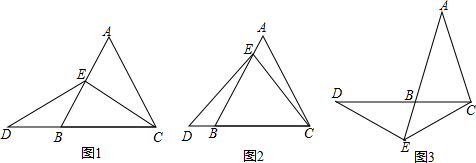
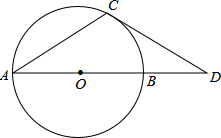 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点.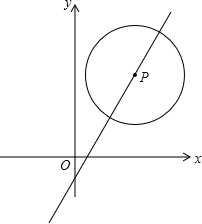 如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动. 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.