题目内容
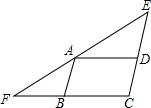 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.(1)求证:△EFC是等腰三角形;
(2)求EC+FC.
考点:平行四边形的判定与性质,等腰三角形的判定与性质
专题:
分析:(1)由平行线的性质可证得∠E=∠F,可证得△EFC为等腰三角形;
(2)由(1)可得AB=FB,且四边形ABCD为平行四边形,可得FC=AB+AD,可求得EC+FC.
(2)由(1)可得AB=FB,且四边形ABCD为平行四边形,可得FC=AB+AD,可求得EC+FC.
解答:(1)证明:
∵AB∥EC,AD∥FC,
∴∠FAB=∠E,∠EAD=∠F,
又∠EAD=∠FAB,
∴∠E=∠F,
∴CE=CF,
∴△EFC是等腰三角形;
(2)解:
由(1)可知∠BAF=∠F,
∴AB=BF,
又AB∥EC,AD∥FC,
∴四边形ABCD为平行四边形,
∴BC=AD=b,
∴CF=FB+BC=AB+BC=AB+AD=a+b,
又CE=CF,
∴EC+FC=2(a+b).
∵AB∥EC,AD∥FC,
∴∠FAB=∠E,∠EAD=∠F,
又∠EAD=∠FAB,
∴∠E=∠F,
∴CE=CF,
∴△EFC是等腰三角形;
(2)解:
由(1)可知∠BAF=∠F,
∴AB=BF,
又AB∥EC,AD∥FC,
∴四边形ABCD为平行四边形,
∴BC=AD=b,
∴CF=FB+BC=AB+BC=AB+AD=a+b,
又CE=CF,
∴EC+FC=2(a+b).
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列说法不正确的是( )
| A、等腰三角形两腰上的中线相等 |
| B、等腰三角形两底角平分线相等 |
| C、等腰三角形的高,中线,角平分线互相重合 |
| D、等边三角形的高,中线,角平分线互相重合 |
 如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
 如图,已知BC是⊙O的直径,点D为BC延长线上一点,点A为圆上一点,AB=AD,∠ADB=30°.
如图,已知BC是⊙O的直径,点D为BC延长线上一点,点A为圆上一点,AB=AD,∠ADB=30°.
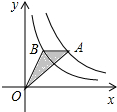 反比例函数y=
反比例函数y= 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°.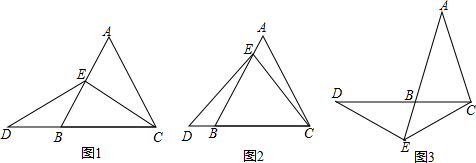
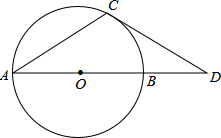 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点.