题目内容
 如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.
如图,在△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,E是边CA上任意一点,DF⊥DE,交BC于F点.G为EF的中点,连接CG并延长交AB于点H.(1)说明:AE=CF;
(2)连接DG,说明:CG=GD;
(3)若AE=1,CH=4,求边AC的长.
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:(1)通过全等三角形(△AED≌△CFD)的对应边相等证得AE=CF;
(2)根据Rt△ECF和Rt△EDF斜边上中线的性质来证明CG=GD;
(3)求出EF的长是4,在Rt△ECF中,CF=1,根据勾股定理求出EC,即可求出AC.
(2)根据Rt△ECF和Rt△EDF斜边上中线的性质来证明CG=GD;
(3)求出EF的长是4,在Rt△ECF中,CF=1,根据勾股定理求出EC,即可求出AC.
解答:解:(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵CD为AB边上的中线,
∴CD⊥AB,AD=CD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCB,
即∠A=∠DCF,
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠CDF+∠EDC=90°,
∴∠ADE=∠CDF,
在△AED和△CFD中,
∴△AED≌△CFD(ASA),
∴AE=CF;
(2)∵∠ACB=90°,G为EF的中点,
∴CG=
EF,
∵DF⊥DE,G为EF的中点,
∴GD=
EF,
∴CG=GD;
(3)∵AC=BC,CD是AB边上的中线,
∴CD⊥AB,
∴∠CDA=90°,
∴∠CHD+∠DCH=90°,∠CDG+∠HDG=90°,
∵CG=DG,
∴∠CDG=∠GCD,
∴∠GDH=∠GHD,
∴DG=GH,
∴CG=GH=
CH=2,
∵G为EF的中点,
∴DG=
EF,
∴EF=4,
∵AE=1,
∴CF=AE=1,
在Rt△ECF中,由勾股定理得:
CE=
=
,
∴AC=CE+AE=
+1.
∴∠A=∠B=45°,
∵CD为AB边上的中线,
∴CD⊥AB,AD=CD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCB,
即∠A=∠DCF,
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠CDF+∠EDC=90°,
∴∠ADE=∠CDF,
在△AED和△CFD中,
|
∴△AED≌△CFD(ASA),
∴AE=CF;
(2)∵∠ACB=90°,G为EF的中点,
∴CG=
| 1 |
| 2 |
∵DF⊥DE,G为EF的中点,
∴GD=
| 1 |
| 2 |
∴CG=GD;
(3)∵AC=BC,CD是AB边上的中线,
∴CD⊥AB,
∴∠CDA=90°,
∴∠CHD+∠DCH=90°,∠CDG+∠HDG=90°,
∵CG=DG,
∴∠CDG=∠GCD,
∴∠GDH=∠GHD,
∴DG=GH,
∴CG=GH=
| 1 |
| 2 |
∵G为EF的中点,
∴DG=
| 1 |
| 2 |
∴EF=4,
∵AE=1,
∴CF=AE=1,
在Rt△ECF中,由勾股定理得:
CE=
| 42-12 |
| 15 |
∴AC=CE+AE=
| 15 |
点评:本题考查了等腰直角三角形的性质、全等三角形的判定与性质、直角三角形斜边上1的中线性质以及勾股定理等知识的综合运用,考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、等腰三角形两腰上的中线相等 |
| B、等腰三角形两底角平分线相等 |
| C、等腰三角形的高,中线,角平分线互相重合 |
| D、等边三角形的高,中线,角平分线互相重合 |
 看图填空:
看图填空: 根据二次函数y=ax2+bx+c的图象草图回答下列问题:
根据二次函数y=ax2+bx+c的图象草图回答下列问题: 反比例函数y=
反比例函数y= 如图,?ABCD的周长是36,由钝角顶点D向AB、BC引两条角DE、DF,且DE=4,DF=6,求这个平行四边形的面积.
如图,?ABCD的周长是36,由钝角顶点D向AB、BC引两条角DE、DF,且DE=4,DF=6,求这个平行四边形的面积. 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°.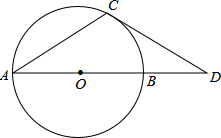 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.