题目内容
 如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为
如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为考点:垂径定理,勾股定理
专题:
分析:连接OP,作OP⊥EF交⊙O于点E、F,则弦EF即为最短的弦,连接OF,根据勾股定理求出PF的长,进而可得出结论.
解答: 解:连接OP,作OP⊥EF交⊙O于点E、F,则EF=2PF.
解:连接OP,作OP⊥EF交⊙O于点E、F,则EF=2PF.
∵OF=4,OP=2,
∴PF=
=
=2
,
∴EF=2PF=4
.
故答案为:4
.
 解:连接OP,作OP⊥EF交⊙O于点E、F,则EF=2PF.
解:连接OP,作OP⊥EF交⊙O于点E、F,则EF=2PF.∵OF=4,OP=2,
∴PF=
| OF2-OP2 |
| 42-22 |
| 3 |
∴EF=2PF=4
| 3 |
故答案为:4
| 3 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是( )
| A、直角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°. 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点.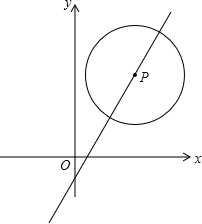 如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动. 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点. 如图,AM是△ABC外接圆的直径,△ABC的高AD的延长线交圆O于点N,求证:BN=CM.
如图,AM是△ABC外接圆的直径,△ABC的高AD的延长线交圆O于点N,求证:BN=CM. 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.