题目内容
9.将关于x的一元二次方程4ax(x-1)=4a2x-1化为一般形式,其一次项系数与常数项相等,则a的值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{7}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
分析 首先去括号,移项,再合并同类项可得4ax2-(4a+4a2)x+1=0,再根据题意可得-(4a+4a2)=1,再解即可.
解答 解:4ax(x-1)=4a2x-1,
4ax2-4ax=4a2x-1,
4ax2-(4a+4a2)x+1=0,
∵一次项系数与常数项相等,
∴-(4a+4a2)=1,
解得:a=-$\frac{1}{2}$,
故选:D.
点评 此题主要考查了一元二次方程的一般式,关键是掌握一元二次方程的一般形式为ax2+bx+c=0(a≠0).其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫一次项系数;c叫做常数项.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
20.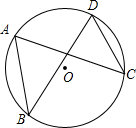 如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )
如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )
 如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )
如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )| A. | 在⊙O上 | B. | 在⊙O内 | C. | 在⊙O外 | D. | 不能确定 |
18.已知a=($\frac{1}{2}$)-2,b=(-2)3,c=(x-2)0,则a,b,c的大小关系为( )
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<c<b |
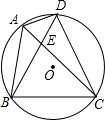 如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.
如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.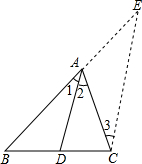 请阅读下面的材料,并回答所提出的问题.
请阅读下面的材料,并回答所提出的问题.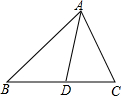
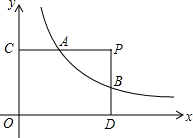 如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.
如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.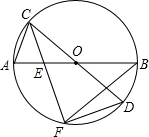 如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF
如图,AB、CD为⊙O的直径,E为OA的中点,直线CE交⊙O于另一点F,连接DF,若⊙O的半径为4,DF=$\sqrt{15}$,CE<EF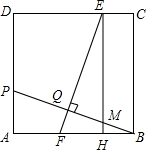 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.