题目内容
1.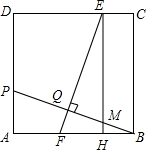 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段AF的长.
分析 (1)由正方形的性质和已知条件可分别证明∠FEH=∠PBA,AB=HE,进而可证明△ABP≌△HEF,由全等三角形的性质即可得到HF=AP;
(2)连接,设AF=x,则PF=BF=12-x,在△APF中利用勾股定理可得:42+x2=(12-x)2,解方程求出x的值即可.
解答 解:(1)∵EF⊥BP,EH⊥AB,
∴∠FEH+∠EMQ=90°=∠PBA+∠BMH,
又∵∠QME=∠BMH,
∴∠FEH=∠PBA,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD,
∵EH⊥AB,
∴∠EHA=90°=∠A=∠D,
∴四边形ADEH是矩形,
∴AD=EH,
又∵AB=AD,
∴AB=EH,
在△ABP与△HEF中
$\left\{{\begin{array}{l}{∠A=∠FHE}\\{AB=HE}\\{∠ABP=∠HEF}\end{array}}\right.$,
∴△ABP≌△HEF(ASA),
∴AP=FH;
(2)连结PF,
∵EF垂直平分BP,
∴PF=BF,
设AF=x,则PF=BF=12-x,
∴在△APF中,42+x2=(12-x)2,
∴x=$\frac{16}{3}$,
∴AF=$\frac{16}{3}$.
点评 本题考查的是正方形的性质、勾股定理的运用、全等三角形的判定和性质以及线段垂直平分线的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.一元二次方程x2+x+4=0在实数范围内的两根之积与两根之和的差是( )
| A. | 5 | B. | -5 | C. | 3 | D. | 不存在 |
9.将关于x的一元二次方程4ax(x-1)=4a2x-1化为一般形式,其一次项系数与常数项相等,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{7}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
6.下列函数是一次函数的是( )
| A. | y=kx+2 | B. | y=-$\frac{6}{x}$ | C. | y=-3x2+2 | D. | y=-$\frac{x}{4}$ |
11.方程-2x+3=0的解是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
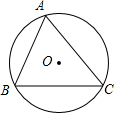 如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.
如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.