��Ŀ����
17��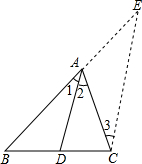 ���Ķ�����IJ��ϣ����ش�����������⣮
���Ķ�����IJ��ϣ����ش�����������⣮�������ڽ�ƽ�������ʶ����������ε��ڽ�ƽ���߷ֶԱ����õ������߶κ�����ǵ����߶�Ӧ�ɱ�����
��֪����ͼ����ABC�У�AD�ǽ�ƽ���ߣ���֤��$\frac{BD}{DC}=\frac{AB}{AC}$
������Ҫ֤$\frac{BD}{DC}=\frac{AB}{AC}$��һ��ֻҪ֤BD��DC��AB��AC��BD��AB��DC��AC���ڵ����������ƣ�����B��D��C��һֱ���ϣ���ABD���ADC�����ƣ���Ҫ�����ñ�ķ������ȣ�
�ڱ���ʽ$\frac{BD}{DC}=\frac{AB}{AC}$�У�ACǡ��BD��DC��AB�ĵ��ı�������Կ��ǹ�C��CE��AD����BA���ӳ�����E���Ӷ��õ�BD��DC��AB�ĵ��ı�����AE��������֤��$\frac{BD}{DC}=\frac{AB}{AC}$�Ϳ���ת��Ϊ֤AE=AC��
��1��֤������C��CE��DA����BA���ӳ�����E�����������֤�����̣�
��AE=AC�ȽǶԵȱ�
���BAD�ס�BEC����$\frac{BD}{BC}=\frac{AB}{BE}$���������ζ�Ӧ�߳ɱ���
��$\frac{BD}{DC}=\frac{AB}{AC}$
��2�����������ڽ�ƽ�������ʶ���������⣺
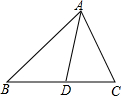
��֪����ͼ����ABC�У�AD�ǽ�ƽ���ߣ�AB=5cm��AC=4cm��BC=7cm����BD�ij���
���� ��1����C��CE��DA����BA���ӳ�����E��������ֱ��ƽ���ڴ��ǡ�ͬλ����ȵõ����Խ���ȣ�����ADΪ��ƽ���ߣ��õ�һ�Խ���ȣ������������ȽǶԵȱߵõ�AE=AC����������BAD��������BEC���ƣ������Ƶñ����������������ɵ�֤��
��2�����ã�1���еĽ��ۣ����BD�ij����ɣ�
��� ��1��֤������C��CE��DA����BA���ӳ�����E��
���2=��3����1=��E��
��ADƽ�֡�BAC��
���1=��2��
���1=��3��
���E=��3��
��AE=AC���ȽǶԵȱߣ���
���BAD�ס�BEC��
��$\frac{BD}{BC}$=$\frac{AB}{BE}$�����������ζ�Ӧ�߳ɱ�������
��$\frac{BD}{BC}$=$\frac{AB}{AC}$��
�ʴ�Ϊ���ȽǶԵȱߣ����������ζ�Ӧ�߳ɱ�����
��2���⣺�ߡ�ABC�У�AD�ǽ�ƽ���ߣ�
��$\frac{AB}{AC}$=$\frac{BD}{CD}$��
��AB=5cm��AC=4cm��BC=7cm��
��$\frac{5}{4}$=$\frac{BD}{7-BD}$��
��ã�BD=$\frac{35}{9}$cm��
���� ���������������ۺ��⣬�漰��֪ʶ�У����������ε��ж������ʣ�ƽ���ߵ����ʣ����������ε��ж���Ū�����н�ƽ�������ʶ����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
12��һԪ���η���x2+x+4=0��ʵ����Χ�ڵ�����֮��������֮�͵IJ��ǣ�������
| A�� | 5 | B�� | -5 | C�� | 3 | D�� | ������ |
9��������x��һԪ���η���4ax��x-1��=4a2x-1��Ϊһ����ʽ����һ����ϵ���볣������ȣ���a��ֵΪ��������
| A�� | $\frac{1}{2}$ | B�� | -$\frac{7}{2}$ | C�� | 0 | D�� | -$\frac{1}{2}$ |
6�����к�����һ�κ������ǣ�������
| A�� | y=kx+2 | B�� | y=-$\frac{6}{x}$ | C�� | y=-3x2+2 | D�� | y=-$\frac{x}{4}$ |
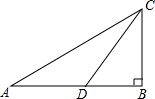 ��ͼ��Rt��ABC�У���ABC=90�㣬��D��ֱ�DZ�AB�ϣ��ҡ�DCB=��A��
��ͼ��Rt��ABC�У���ABC=90�㣬��D��ֱ�DZ�AB�ϣ��ҡ�DCB=��A��