题目内容
19.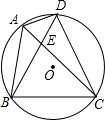 如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.
如图,四边形ABCD内接于⊙O,连接AC和BD相交于E,且AC平分∠BAD,求证:BC2=AC•CE.
分析 根据已知条件及相似三角形的判定方法结合图形和圆周角定理即可证明△ABC∽△BCE,然后根据相似三角形的性质即可得到结论.
解答 证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,BC=CD,
∴∠DAC=∠CDE,∠BDC=∠DBC,
∴∠DBC=∠BAC,
∵∠DCE=∠ACD,∠ACB=∠BCE,
∴△ABC∽△BEC,
∴$\frac{AC}{BC}=\frac{CE}{BC}$,
∴BC2=AC•CE.
点评 本题考查了相似三角形的判定:
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.

练习册系列答案
相关题目
9.将关于x的一元二次方程4ax(x-1)=4a2x-1化为一般形式,其一次项系数与常数项相等,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{7}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
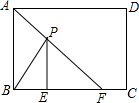 如图,在矩形ABCD中,AB=4cm,AD=5cm,点E在BC边上,且BE=1cm,AF平分∠BAD,图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为5cm.
如图,在矩形ABCD中,AB=4cm,AD=5cm,点E在BC边上,且BE=1cm,AF平分∠BAD,图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为5cm.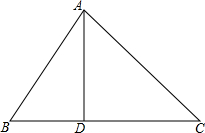 如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.
如图,D是△ABC中BC边上一点,∠B=∠DAC,AB2=BD•BC.求证:△ABD∽△CAD.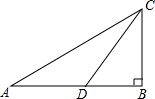 如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A.
如图,Rt△ABC中,∠ABC=90°,点D在直角边AB上,且∠DCB=∠A.