题目内容
4.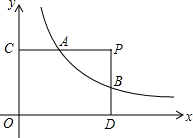 如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.
如图,点P(a,b)在第一象限内,PC⊥y轴于点C,PD⊥x轴于点D,两条垂线交反比例函数y=$\frac{k}{x}$的图象于点A、B.(1)分别写出A、B两点的坐标(用a,b,k表示);
(2)求证:$\frac{PA}{PC}$=$\frac{PB}{PD}$.
分析 (1)根据P(a,b),PC⊥y轴于点C,PD⊥x轴于点D,于是得到A点的纵坐标与P点的纵坐标相同,B点横坐标与P点的横坐标相同,由于A、B在反比例函数y=$\frac{k}{x}$的图象上,即可得到结论;
(2)通过P,A,B点的坐标得到CA=$\frac{k}{b}$,PC=a,PD=b,DB=$\frac{k}{a}$,根据对应线段的比相等得到结论.
解答 (1)解:P(a,b),PC⊥y轴于点C,PD⊥x轴于点D,
∴A点的纵坐标与P点的纵坐标相同,B点横坐标与P点的横坐标相同,
∵A、B在反比例函数y=$\frac{k}{x}$的图象上,
∴A($\frac{k}{b}$,b),B(a,$\frac{k}{a}$);
(2)证明:∵P(a,b),A($\frac{k}{b}$,b),B(a,$\frac{k}{a}$),
∴CA=$\frac{k}{b}$,PC=a,PD=b,DB=$\frac{k}{a}$,
则PA=PC-CA=a-$\frac{k}{b}$,PB=PD-DB=b-$\frac{k}{a}$,∴$\frac{PA}{PC}$=$\frac{a-\frac{k}{b}}{a}$=$\frac{ab-k}{ab}$,$\frac{PB}{PD}$=$\frac{b=\frac{k}{a}}{b}$=$\frac{ab-k}{ab}$,
∴$\frac{PA}{PC}$=$\frac{PB}{PD}$.
点评 本题考查了反比例函数的综合题,关键是利用P点坐标,点与点的坐标关系,反比例函数的性质表示相关线段的长得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一元二次方程x2+x+4=0在实数范围内的两根之积与两根之和的差是( )
| A. | 5 | B. | -5 | C. | 3 | D. | 不存在 |
19.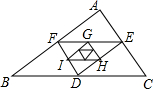 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
9.将关于x的一元二次方程4ax(x-1)=4a2x-1化为一般形式,其一次项系数与常数项相等,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{7}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
14.方程|x-3|=6的解是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | 9或-3 |
 如图,△ABC中,∠ACB=90°,CD⊥AB于D,E为AC的中点,ED、CB的延长线交于点F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,E为AC的中点,ED、CB的延长线交于点F.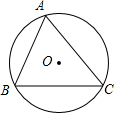 如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.
如图,⊙O是△ABC的外接圆,⊙O的半径是R=2,sinA=0.8,则弦BC的长为3.2.