Question

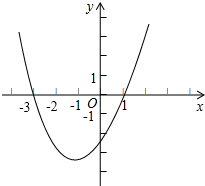阅读材料，解答问题．
利用图象法解一元二次不等式：x²+2x-3＜0．
解：设y=x²+2x-3，则y是x的二次函数．∵a=1＞0，
∴抛物线开口向上．
又∵当y=0时，x²+2x-3=0，解得x₁=1，x₂=-3．
∴由此得抛物线y=x²+2x-3的大致图象如图所示．
观察函数图象可知：当-3＜x＜1时，y＜0．
∴x²+2x-3＜0的解集是：-3＜x＜1时．
（1）观察图象，直接写出一元二次不等式：x²+2x-3＞0的解集
（2）仿照上例，用图象法解一元二次不等式：-2x²-4x+6＞0．

Answer 1

考点：二次函数与不等式（组）

专题：

分析：（1）根据函数图象，写出抛物线在x轴上方部分的x的取值范围即可；
（2）先判断出抛物线开口向下，再令y=0求出抛物线与x轴的交点的横坐标，然后写出抛物线在x轴上方部分的x的取值范围即可．

解答：解：（1）x²+2x-3＞0的解集是x＞1或x＜-3；

（2）设y=-2x²-4x+6，则y是x的二次函数，
∵a=-2＜0，
∴抛物线开口向下，
又∵当y=0时，-2x²-4x+6=0，解得x₁=1，x₂=-3．
∴由此得抛物线y=x²+2x-3的大致图象如图所示，
观察函数图象可知：当-3＜x＜1时，y＜0．
∴-2x²-4x+6＞0的解集是：-3＜x＜1时．

点评：本题考查了二次函数与不等式，读懂题目信息，理解一元二次不等式的求解方法是解题的关键．