题目内容
13. 如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )
如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
分析 连接OB、OC,由圆周角定理得出∠BOC=2∠BAC=100°,由等腰三角形的性质得出∠OCF=40°,由折叠的性质得出OC⊥EF,即可求出∠CFE的度数.
解答 解:连接OB、OC,如图所示:
由圆周角定理得:∠BOC=2∠BAC=100°,
∵OB=OC,
∴∠OCF=$\frac{1}{2}$(180°-100°)=40°,
由折叠的性质得:OC⊥EF,
∴∠CFE=90°-40°=50°;
故选:C.
点评 本题考查了三角形的外接圆与外心、圆周角定理、等腰三角形的性质、折叠的性质;熟练掌握三角形的外心性质和折叠的性质,由圆周角定理求出∠BOC是解决问题的关键.

练习册系列答案
相关题目
8. 如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )
如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )
 如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )
如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )| A. | 24° | B. | 33° | C. | 42° | D. | 43° |
18. 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )| A. | 矩形 | B. | 菱形 | C. | 矩形或菱形 | D. | 正方形 |
 如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.
如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.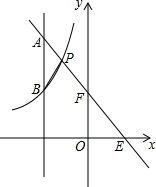 如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图: